S：足し算みたいだけれどちょっと違う。
Ｔ：０，１，２，３の４つの数はそれだけで‘@’について世界を作っているよ。２@３＝５じゃなくて１だもんね。
S：この表さえ使えば勝てるけど，計算で出すにはどうしたらいいの？
Ｔ：右の表を見て、何か気がつきませんか。
S：右の表は繰り上がりのない足し算だ！
S：わかった。二進数にするとわかる。これで、必ず勝てるぞ。
S：でもなぜ二進法の計算なんだろう？
S：この表を８まで作ってみると、｛０,１,…２ｎ−１｝は群になっているよ。
S：つまり、ｐ＜８なら、ｐ＠８＝ｐ＋８ということだ。ということは、ｐを２の累乗の和で表すと、普通の加法の組み合わせで計算できるということか。
石とりゲーム（三山くずし）・・・いくつにすれば良いか計算
この変換ソフトで計算してみてください。
このソフトは１０進数は５桁まで、２進数は１６桁まで求めることができます。
数字を入れてから変換ボタンを押してください。
参考文献 「石とりゲームの数理」一松信著/森北出版
三人ゲーム
-------------------------------------------------------------------
Ｔ：今までは山を増やしていったけれど，今度はゲームをする人数を増やしてみよう。最初の一山の場合の「１６減らし」を３人でやるとどうなるか？
（１，２，３，４，５，６，７，８，９，１０，１１，１２，１３，１４，１５，１６）
-------------------------------------------------------------------
三人でやってみよう！
S：このまま３とればあいつが負けるから１つにして，次のやつを負かせよう。
エッ！みんなが一ずつ取ったら俺の負けじゃないか。
S：えーと，２人を相手にするのだから最低２から６までの数を減らされると考えると，・・・。
S：２を取るためには２人が９で終わらなくてはならない。でも，自分は三個しか取れない。
S：次の人がいくつ取ってもその次の人が１を残せるから必ず負けるな。
S：２人を相手にするから難しくなるんだ。みんな別々と考えると・・・
S：さっきの「２×奇数の法則」を使っても，三人だと順番が変わるから必ず勝てるとは限らない。それに，相手はこの法則を相手に使わせる様にするかもしれない。
Ｔ：どうだい。２人ゲームを３人にすると，とたんにゲームが難しくなることがわかったかい。昔から三角関係は難しいと言われていているんだ。とりあえず，いろいろやってみよう。何か法則が見つかるかもしれない。
S：わかった。一人で勝とうと思っても二人相手には負けるんだから，誰かと組めば必ず一人を負かすことができる。
S：本当に負かせるの？説明してみて。
S：負かしたい人が２と３を取ると，味方のどちらかが負ける。この二つを取らせないようにすることは，二人で協力すれば必ずできる。２と３さえとらせなければ負かすことができる。
S：つまり，三人の場合は一人だけで勝つことはできないけど，二人で協力すれば一人を必ず負かすことはできるということだ。
S：三人でゲームをする場合は，誰か一人と組んで，そのあとその一人をやっつければ良いわけか。何だか三人でやる喧嘩にも当てはまりそう。
S：敵の敵は味方というわけか。でも誰と組むか問題になるな。お互いにそう考えたらどうなるんだろう。
Ｔ：そうなると人間関係の問題だね。
S：じゃ四人になるとどうなるのかな。
Ｔ：数学は現象の「法則を見つける」学問なんだ。今までやったように，法則を見つければ勝負に有利になるね。
経済や政治などを一種のゲームとしてとらえ，それを簡単なモデルにしてプレーヤーがどう行動したら最も良いのかを考える理論は，「ゲームの理論」 Game Theoryとして発展しています。（意思決定の数学として生活上でもいろいろ使えます。勉強してみて下さい。）
S：今までのゲームで考えてきたことも数学なの？
Ｔ：もちろん。時々なぜかと聞いたのは証明ですよ。
S：ボクはいつもプレイステーションをやっているから数学をやっているといっても良いんだね。
Ｔ：ン？
S：ゲームの理論では戦争もゲームととらえるんでしょう。
Ｔ：平和を追求するためには、戦争を知らなきゃいけない。どうして戦争が起きたのか、その戦争の結果はどうなったのか、というようなことを研究することは大事だよね。でも、それを何のために研究するのかということは忘れてはならないよ。数学はいつも戦争で使われてきた歴史がある。
S：コンピュータは戦争で使うために生まれたんでしょう。
Ｔ：ところで、戦略の中にモノマネ戦略というのがある。それは、最初は友好的な手をうち、次は相手と同じ手をうつというもの。相手が裏切ったら裏切り、協力しようとしたら協力するという戦略なのだ。コンピュータのシュミレーションでは、今のところこの単純な戦略が一番成績が良いらしい。生き物の進化の戦略も、案外こういった単純なモノかもしれないよ。
Ｔ：「三山くずし」の時には、法則というよりもこの表の中に何か構造が隠されていることに気がつくね。この表の演算を‘@’という計算だと考えると、その演算がどういう構造（しくみ）になっているのかという問題になってくる。このように数学には「現象の構造をつかむ」という面もあります。構造がわかるとゲームでは有利になるでしょう。
S：構造も法則じゃないの？
Ｔ：少し違うんだな。
Ｔ：こんどは法則よりも構造が問題になるゲームをやってみよう。
彼女を追いかけろ
-------------------------------------------------------------------
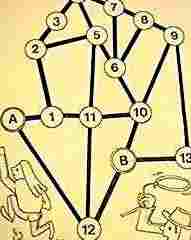Ｔ：次の図を見てください。「彼女を追いかけろ」というゲームです。これは２人でやるゲームで，最初はＡとBにいてAから追いかけます。Bは逃げますが，１つしか進むことができません。追いつけば勝ちです。
-------------------------------------------------
(3)の上が消えていますが，これは(4)です。「pdf 拡大画像」
さあ，やってみようか。君の方から追いかけてみて。何かを置いてやってみると分かりやすいよ。
（(1)に行くと(12)に逃げる。(11)に行くとAに逃げる。(12)に行くと(1)に逃げる。）
S：こんなの絶対追いつくことができないよ。
Ｔ：じゃ，今度は私が追いかけてみようか。
S：あれ？つかまっちゃった。どうして？
Ｔ：ちゃんとつかまるでしょう。 （内緒！(7)(8)を通れば必ず捕まえられる。）
S：今度は私が追いかけてみる。あれ，つかまらない。どうして？もう一度やってみて。
S：またつかまっちゃった。この数字の順番に追いかければつかまえれるのかな。
Ｔ：こんどは先に逃げてごらん。必ずつかまるよ。
S：本当だ。逃げるとつかまり，追えばつかまらない。どうして？
Ｔ：これはこの図の構造に秘密があるんですよ。それを解くためには，次のグラフを使って図を簡単にするのです。やってみましょう。これは横浜国大の根上さんの「グラフ理論」のページです。 gm learning のページへリンク。クリックしてページを開いてみてください。
(1) 開始ボタンを押すとgm applet が開きます。
(2) 右クリックすると点が描けます。
(3) 次は線を結びます。それは点を右クリックして結びたい次の点の位置にカーソルを持っていって右クリックすると線が引けます。
(4) 上の図を見て，点を１５個とり，線を結んでみてください。
(5) 位置関係を間違えないように図を作ってください。
(6) できたら，この図（グラフ）の点を動かします。
(7) どう動かすかが問題ですが，動かしているとこの図（グラフ）の構造が見えてくるのです。
やってみましょう。 【ジオジェブラによる「彼女を追いかけろ」の並べ直し】
でたらめに点を動かしたってだめですよ。ちゃんと整理しなくては。
どうですか。グラフの点を動かしているうちにこのグラフの構造がわかり，したがってなぜ追いつくのかもわかってしまいましたね。
S：なんだ、このグラフは格子になるのか。そして、(7)と(8)の所がつながっている。つまり、ひとつ跳んで進んでいるわけだ。ひとつ進めば必ず追いつくよ。
Ｔ：どうやらこの図の構造がつかめたようですね。この上の図は，伸ばしたり縮めたりしてわからなくさせているだけなんですね。この様に図（グラフ）のつながりを探っていくという数学もあるんですよ。
さらに興味のある人は簡単な「グラフ理論」を学んでみましょう。さっきの根上さんのホームページです。数式や計算はでてきません。マウスを動かしながら「グラフ理論」が学べます。
次の項目をクリックしてみて下さい。