亀寁嶼婡傕僽儔僢僋儃僢僋僗偩亁
丂偙偺寁嶼婡傕僽儔僢僋儃僢僋僗偺堦偮偱偡丅偨偲偊偽丄俀傪擖椡偟傑偡丅偦偟偰丄亊偲亖傪墴偡偲丄係偵側傝傑偡丅偝偰丄偙偺僉乕偼偳傫側摥偒傪偟偰偄傞偺偐摉偰偰傒偰偔偩偝偄丅
丒丒俀攞偡傞摥偒丅
傕偟偦偆側傜丄俁傪擖椡偡傞偲丠
丒丒俇偵側傞丅偁傟両丂俋偩丅
偱偼丄係傪擖椡偡傞偲丠
丒丒侾俇偱偡丅
偙偺亊亖偼偳偆偄偆摥偒傪偟偰偄傞偺丅
丒丒俀夞偐偗傞摥偒丅
丒丒俀忔偡傞摥偒丅
丒丒暯曽偡傞摥偒丅
丒丒惓曽宍偺侾曈偐傜柺愊傪弌偡摥偒丅
丒丒倄亖冊亊冊
師偼丄併偲偄偆僉乕傪挷傋傑偡丅偙偺僉乕偺摥偒傪抦偭偰偄傞偐偄丅
丒丒抦傝傑偣傫丅
偨偲偊偽丄係傪擖椡偟偰併傪墴偡偲弌椡偼俀偵側傞丅偳偆偄偆摥偒傪偟偰偄傞丅
丒丒俀偱妱傞丅
偠傖丄俋傪擖椡偡傞偲丄係丏俆偲偄偆偙偲丠丂偼偄丄併傪墴偡偲丄巆擮偱偟偨丅俁偱偡丅
丒丒丠
俀俆傪擖椡偡傞偲丠
丒丒俆偩丅
偦偺捠傝丅偲偙傠偱偳偆傗偭偰寁嶼偟偨偺丅
丒丒夝傜側偄丅
丒丒俀忔偟偰俀俆偵側傞悢傪媮傔傑偟偨丅
偱偼丄偙偺併偺摥偒偼丅
丒丒俀忔乮暯曽乯偺斀懳偺摥偒丅
丒丒俀夞偐偗偰侾俇偵側傞悢傪弌椡偡傞摥偒丅
丒丒惓曽宍偺柺愊偐傜侾曈傪弌偡摥偒丅
偙偺併偺摥偒傪暯曽崻傪媮傔傞摥偒偲偄偄丄併偺偙偲傪儖乕僩偲偄偄傑偡丅
偱偼丄俀傪擖椡偟偰併傪墴偡偲偳傫側悢偑弌椡偝傟傑偡偐丅
丒丒偊乕偲丄侾偲俀偺娫偺悢丅
丒丒侾丏係侾係俀侾俁俆俇俀偩偭偰丅
丒丒俀忔偟偰傕俀偵側傜側偄傛丅侾丏俋俋俋俋俋俋俋俋俉偵側偭偰偄傞丅偳偆偟偰丠
乮俀傪擖椡偟偰丄併傪墴偡丅
侾丏係侾係俀侾俁俆俇俀偲弌偰偔傞偺偱丄偦偺傑傑亊亖傪墴偡丅
偡傞偲丄侾丏俋俋俋俋俋俋俋俋俉偲弌偰偔傞丅乯
偄偄幙栤偩側偁丅偳偆偟偰側偺偐丄峫偊偰傒傛偆丅
丒丒偪傚偭偲丄彫偝偐偭偨傫偠傖側偄偺丅
偱偼丄侾丏係侾係俀侾俁俆俇俁傪俀忔偟偰傒傛偆丅
丒丒俀丏侽侽侽侽侽侽侽侽侾偵側偭偨傛丅偙傟偱偼戝偒偡偓傞傫偩丅
丒丒偲偄偆帠偼丄侾丏係侾係俀侾俁俆俇俀丒偲傑偩懕偔傫偩丅
偳偙傑偱懕偔偺丠
丒丒柍尷偵懕偒傑偡丅
棟桼偼尵偊傑偡偐丅
丒丒傕偟丄偳偙偐偱廔傢傞偲偡傞偲侾偐俀偐俁偐係偐俆偐俇偐俈偐俉偐俋偺偳傟偐偺偼偢丅偙傟偼俀忔偡傞偲俀偵側傜側偔偰偼偄偗側偄偗偳丄侾傪俀忔偟偰傕侾丄俀傪俀忔偟偰傕係丄俁傪俀忔偟偰傕俋丄係傪俀忔偟偰傕俇丄俆傪俀忔偟偰傕俆丄俇傪俀忔偟偰傕俇丄俈傪俀忔偟偰傕俋丄俉傪俀忔偟偰傕係丄俋傪俀忔偟偰傕侾偼昁偢巆傞丅
偩偐傜丄俀忔偟偰傕俀偵偼寛偟偰側傜側偄丅偦偆偡傞偲丄
偳偙偐偱廔傢傞偲偄偆偙偲偼側偄偐傜丄柍尷偵懕偔彮悢偵側傝傑偡丅
丒丒偡偛偄丅
偙傟傪丄俀偺暯曽崻偲偄偄丄彮悢偱昞傢偡偲惓妋偵偼昞傢偣側偄偺偱丄併俀偱昞傢偟傑偡丅偙偆偄偆悢傪柍棟悢偲偄偄傑偡丅
丒丒俁偺暯曽崻偼併俁側傫偱偡偹丅
丂亀併俀偑偙傫側強偵偁傞丅亁
丒丒併俀偭偰丄壗偺栶偵棫偮傫偱偡偐丅
傛偔偧暦偄偰偔傟傑偟偨丅偙偙偵庢傝偄弌偟傑偟偨傞峏巻偵偼丄併俀偑偁傞丅
丒丒尒偊傑偣傫傛丅
偱偼丄偙傟傪敿暘偵愗偭偰傒傛偆丅偳偆偱偡偐丄併俀偑尒偊傑偟偨偐丅

丒丒偄偭偙偆偵丅
偱偼丄侾枃巆偟偰丄傕偆堦枃傪敿暘偵偟偰偔偩偝偄丅
傑偨侾枃巆偟偰丄偝傜偵敿暘偵偟偰偔偩偝偄丅偳傫偳傫傗偭偰偄偔偲丄壗偐婥偑偮偒傑偣傫偐丅
丒丒傒傫側宍偑摨偠偱偡丅
偳偙偐傜夝傝傑偟偨偐丅
丒丒暲傋傞偲丄憡帡偱偡丅
偙偙偵丄併俀偑塀偝傟偰偄傞偺偱偡丅偱偼丄偼偭偒傝偲偟偰傒傑偟傚偆丅傑偢丄偙偺侾斣戝偒側挿曽宍偺廲偺挿偝傪侾偲偟傑偡丅墶偺挿偝偼偄偔傜偵側傞偱偟傚偆丅
傑偩傢偐傜側偄偐傜丄倃偲偍偒傑偡丅憡帡偩偐傜斾偺抣偑摨偠偲偄偆偙偲偐傜丄侾丗倃亖倃乛俀丗侾偲偄偆斾偺幃偑偱偒傑偡丅偙偺幃傪夝偄偰傒偰壓偝偄丅
丒丒倃亖亇併俀偵側傝傑偡丅
丒丒偮傑傝丄墶偺挿偝偼廲偺挿偝偺併俀攞偩偭偨偺偐丅
併俀攞側傜偽丄敿暘偵偟偰傕昁偢尦偺宍偲憡帡宍偵側傞偺偱偡丅
丒丒偦傟偱偼丄杮傕併俀攞偵側偭偰偄傞偺偐側丅
丂丂亀俙敾偲俛敾亁
丂
丂杮偺戝偒偝偵偼丄俙偲俛偺擇偮偺宯楍偑偁傝傑偡丅俙楍偼丄柺愊侾噓丄廲墶偺挿偝偺斾侾丗併俀偺俙楍侽斣傪婎杮偲偟丄弴師偺偦偺挿曈傪敿暘偵偟偰偄偭偨傕偺偱丄侾斣偐傜侾俀斣傑偱偁傝傑偡丅俛楍偼丄柺愊侾丏俆噓丄廲墶偺斾傪侾丗併俀偺侽斣傪婎杮偲偟偰丄傗偼傝侾斣偐傜侾俀斣傑
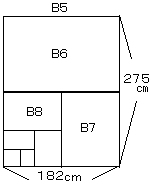 偱偁傝傑偡丅帺暘偺帩偭偰偄傞杮傪挷傋偰傒偰壓偝偄丅
偱偁傝傑偡丅帺暘偺帩偭偰偄傞杮傪挷傋偰傒偰壓偝偄丅丒丒儚乕僋偼丄俛俆敾偱偡丅
丒丒嫵壢彂偼丄俙俆敾偱偡丅
丒丒暥屔敾偼丄俙俇敾偱偡丅
偙偺嫵壢彂偲儚乕僋偺娫偵偼丄柺敀偄娭學偑偁傝傑偡丅
丒丒憡帡埲奜偵偱偡偐丅
偦偆丅偙偺擇偮偺杮偵挿偝偑摨偠強偑偁傞偺偱偡丅
丒丒傢偐偭偨丅嫵壢彂偺懳妏慄偺挿偝偲丄儚乕僋偺廲偺挿偝偑摍偟偄丅
偱偼丄嫵壢彂偺墶偺挿偝傪侾偲偡傞偲丄廲偺挿偝偼丠
丒丒併俀偱偡丅

僺僞僑儔僗偺掕棟傪巊偭偰丄嫵壢彂偺懳妏慄偺挿偝傪弌偟偰傒傑偟傚偆丅
丒丒侾亊侾亄併俀亊併俀亖俁丅偟偨偑偭偰丄併俁偱偡丅
偮傑傝丄儚乕僋偺廲偺挿偝偼併俁偲偄偆偙偲偱偡丅偡傞偲丄
儚乕僋偲嫵壢彂偺挿偝偺斾偼丠
丒丒併俁丗併俀偱偡丅
柺愊偺斾偼丠
丒丒擇忔偟偰丄俁丗俀偱偡丅
丒丒儚乕僋偺曽偑侾.俆攞偲偄偆偙偲偐丅
強偱丄惢杮壆偼側偤丄廲丗墶傪侾丗併俀偵偟偨偺偱偟傚偆丅
丒丒敿暘偵偟偰傕宍偑摨偠側傜丄巻傪愗偭偨帪偵柍懯側偔巊偊傞偐傜偩偲巚偄傑偡丅
亀怴彂敾偲墿嬥斾亁
丒丒愭惗偙偺杮偼侾丗併俀偲偼堘偄傑偡傛丅
偙傟偼怴彂敾偱偡偹丅怴彂敾偼堘偆峫偊曽偱丄憂偭偰偁傝傑偡丅偲偙傠偱丄偙偙偵挿曽宍偑俇庬椶偁傝傑偡丅偳偺挿曽宍偑丄堦斣旤偟偄偲巚偄傑偡偐丅
丒丒墿嬥暘妱偺挿曽宍丗俛敾夋梡巻亖侾俈丗俉
偙偺堦斣懡偐偭偨挿曽宍偑丄怴彂敾偲憡帡側挿曽宍側偺偱偡丅偙偺怴彂敾偼丄偙偺挿曽宍偺廲傪侾曈偲偡傞惓曽宍傪嶌偭偨帪丄巆傝偺挿曽宍偲尦偺挿曽宍偲偑憡帡偵側傞傛偆偵嶌偭偰偁傞偺偱偡丅
丒丒側傫偩偐傗傗偭偙偟偄側丅
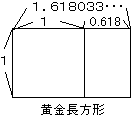
丒丒廲傪侾偲偟丄墶傪倃偲偡傞丅
丒丒惓曽宍傪嶌傞偲丄巆傝偺挿曽宍偺廲偼倃亅侾偱丄墶偼侾丅
丒丒憡帡偩偐傜丄侾丗倃亖倃亅侾丗侾
丒丒曽掱幃偵偡傞偲丄倃乮倃亅侾乯亖侾
丒丒偮傑傝丄倃亊倃亅倃亖侾
丒丒夝偺岞幃傪巊偭偰丄倃亖乮侾亇併俆乯乛俀
丒丒惓偺曽偼丄侾丏俇侾俉侽俁俁俋俆乧
柺敀偄偙偲偵丄侾亐侾.俇侾俉侽俁俁俋俆乧亖侽丏俇侾俉侽俁俁俋俆乧
偲側傞丅偮傑傝彮悢晹暘偼傑偭偨偔摨偠側傫偩丅
丒丒偩偭偰丄恾偱侾傪堷偄偨巆傝偑侽.俇侾俉乧偩偐傜摉慠偠傖側偄丅
偁偭両偦偆偐丅側傞傎偳丅偲偙傠偱偙偺斾偼丄墿嬥暘妱偲偄偭偰丄愄偐傜旤偟偄斾偲偄偆偙偲偑抦傜傟偰偄傞丅
丒丒傎傫偲偵旤偟偄偺偐側丅
偝偭偒丄杮摉偵旤偟偄偲姶偠傞偺偐帋偟偰傒偨偑丄偙偺僋儔僗偼懡偐偭偨偹丅
偙偺墿嬥斾偼侾丗侽.俇俉乮侾丗侾.俇俉偱傕傛偄乯側傫偩偑丄偙偺斾偑偄傠傫側強偵偱偰偔傞丅偙偺斾偼柤巋傗僷儖僥僲儞恄揳丄儌儞僪儕傾儞偺奊丄偦偺懠偺條乆側奊偺拞偵偁傞丅壞媥傒偺尋媶偱丄奊偺拞偺墿嬥暘妱偺椺傪挷傋偰偒偨丄塱堜偝傫偲偄偆惗搆偑偄偨傛丅惓俆妏宍偺摨偠捀揰傪捠傜側偄俀杮偺懳妏慄傕丄屳偵懠傪墿嬥暘妱偡傞丅
丒丒偦傫側偵戲嶳巊傢傟偰偄傞偺偐丅
嶲峫暥專丂丂亀墿嬥暘妱亁桍椇挊丄旤弍弌斉幮
亀嶰妏掕婯偩偭偰偩偰偵嶌偭偰側偄亁
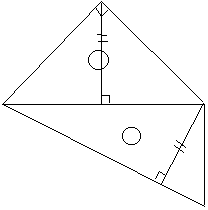
丂捈妏擇摍曈嶰妏宍偺曽偼丄惓曽宍偺敿暘丅傕偆堦偮偺曽偼惓嶰妏宍偺敿暘丅廬偭偰丄俇侽搙偲俁侽搙偵側傞帠偼偡偖夝傞偩傠偆丅
偙偺擇偮偺嶰妏宍偺崅偝偑丄摨偠偱偁傞帠偼埬奜抦傜傟偰偄側偄丅偦傟傪寁嶼偟偰傒傛偆丅偙偺俀偮偺捈妏嶰妏宍偼丄惓曽宍偺懳妏慄偲惓嶰妏宍偺崅偝偑摨偠偵側傞傛偆偵嶌偭偰偁傞丅
丒丒抦傜側偐偭偨丅
丒丒杮摉偵偦偆側偺丅
捈妏俀摍曈嶰妏宍偺崅偝傪侾偲偡傞偲丄惓嶰妏宍偺崅偝偼俀偵側傞偺偱丄幬曈傪掙曈偲偡傞捈妏嶰妏宍偺崅偝偼丄侾偲側傞丅
偙傟傪敪尒偟偨偺偼摗堜孨偲偄偆巕偱丄俀偮偺嶰妏掕婯傪暲傋偰偄偰婥偑偮偄偨偲偄偆丅
丒丒嶰妏掕婯傕偪傖傫偲峫偊偰嶌偭偰偁傞傫偱偡偹丅
偳傫側暔偱傕丄偦傟側傝偺傢偗偑偁偭偰丄嶌傜傟偰偄傞傕傫偩丅
丂亀僪儔僪儔僄儌儞亁
 柤晅偗偰丄僪儔僪儔僄儌儞丅
柤晅偗偰丄僪儔僪儔僄儌儞丅乮僪儔僄儌儞偺奊傪弌偟偰崟斅偵揬傞丅乯
丒丒儚乕丄偐傢偄偄丅
乮偝傜偵丄敿暘偵弅彫偟偨暔傪揬傞丅偳傫偳傫敿暘傪揬傞丅乯
丒丒乮徫偄惡乯傑偩偁傞偺丠
偙偺偙偲偼丄慜偵杮偺戝偒偝偺偲偙傠偱傗偭偨偗偳丄敿暘偵偟偰傕宍偼曄傜側偄丅僐僺乕傪巊偆偲丄偙傟傕娙扨偵偱偒傞丅強偱敿暘偵偡傞偵偼丄弅広傪偳傟偩偗偵偡傟偽偄偄偺丠
丒丒侾丗併俀偩偐傜丄侾亐侾.係侾係俀亖侽.俈侽俈侾丅
丒丒侽.俈侾攞偵偡傟偽偄偄偱偡丅
偱偼丄偙偺堦斣戝偒偄僪儔僪儔僄儌儞偺墶偺挿偝傪侾偲偡傞偲丄師偺僪儔僪儔僄儌儞偺墶偺挿偝偼併俀暘偺侾丅偝傜偵師偺偼丠
丒丒敿暘偩丅
 堦偮偍偒偵偲傞偲丄
堦偮偍偒偵偲傞偲丄丒丒侾丄(侾乛俀)丄(侾乛係)丄(侾乛俉)丄(侾乛侾俇)丅
丒丒敿暘偺敿暘偺敿暘偺丒丒丒
偙傟傪慡晹懌偟偨丄侾亄(侾乛俀)亄(侾乛係)亄(侾乛俉)亄(侾乛侾俇)丒丒丒偺摎偊偼丠
丒丒偙偺暲傋曽傪尒傞偲丄俀偩丅
愄偐傜丄僠儕傕愊傟偽嶳偲側傞偲偄偆偗傟偳丄偙傟傪柍尷偵懌偟偰偄偭偰傕丄嶳偵偼側傜偢偵俀偲側傞傢偗偩丅
丒丒傾僉儗僗偲婽偺榖偲摨偠偩偹丅
偱偼丄墳梡丅
侽.俋亄侽.侽俋亄侽.侽侽俋亄侽.侽侽侽俋亄侽.侽侽侽侽俋丒丒丒亖偄偔偮偵側傞偐
丒丒侽丏俋俋俋俋俋俋俋丒丒丒
偙傟偼偳偆偄偆悢丅偳傫偳傫憹偊偰偄偔偺丅偁傞悢偵側傞偺丅
丒丒偳傫偳傫憹偊傞丅
偳偙傑偱傕憹偊傞偺丅
丒丒偄傗丄侾傛傝偼戝偒偔側傜側偄丅丂侽丏俋俋俋俋俋丒丒丒亙侾偩偐傜丅
堘偆偺偩丅幚偼丄侽丏俋俋俋俋俋俋丒丒丒丒丒亖侾側傫偩丅
丒丒偦傫側偼偢偼側偄丅徹嫆傪尒偣偰丅丂丂丂
偨偲偊偽丄俆偮偺傝傫偛傪俆恖偱傢偗傞偲堦恖壗屄偐丅偦偺摎偼侾丅偟偐偟丄傕偆堦偮摎偑偁傞丅偦傟偼丄
丂丂丂丂丂丂侽丏俋俋俋俋俋俋俋俋俋俋俋俋俋俋乧
丂丂丂俆丂乯俆
丂丂丂丂丂丂侽丂丂
丂丂丂丂丂丂俆丂侽 丂
丂丂丂丂丂丂係丂俆
丂丂丂丂丂丂丂丂俆侽
丂丂丂丂丂丂丂丂係俆
丂丂丂丂丂丂丂丂丂俆侽
偩偐傜丄侾亖侽丏俋俋俋俋俋俋俋俋俋俋丒丒丒
丒丒偍偐偟偄傛丅壗屘丄傢偞傢偞俋偱妱傞偺丅侾偱妱愗傟傞偠傖側偄丅
傝傫偛偵傕偄傠偄傠偁偭偰丄惵偄偺傗愒偄偺丄巁偭傁偄偺傗娒偄偺丄扨弮偵偼妱愗傟側偄丅偙偭偪偺曽偑偄偄偲偐丄偍偄偟偦偆偩偲偐怓乆暥嬪偑偱傞偩傠偆丅偮傑傝丄堦恖偵堦屄偲偄偆傛偆偵娙扨偵偼暘偗傜傟側偄丅偩偐傜丄尷傝側偔侽丏俋俋俋俋俋俋丒丒丒側偺偩丅
丒丒擺摼偱偒側偄側偁丅
偠傖丄徹嫆偺戞俀抏丅侽丏俋俋俋俋俋俋丒丒丒傪侾侽攞偡傞偲丠
丒丒俋丏俋俋俋俋俋俋丒丒丒偱偡丅
俋丏俋俋俋俋俋俋丒丒丒亅侽丏俋俋俋俋俋俋丒丒丒亖
丒丒俋偱偡丅
侾侽攞偟偰堷偄偨傜俋偵側傞悢偼丠
丒丒侾侽刾亅刾亖俋偩偐傜丄偊乕偲刾亖侾偩丅偁傟丠
丒丒偛傑偐偝傟偰偄傞傛丅
偟偐偨偑側偄丅徹嫆偺戞俁抏丅嶰暘偺堦偼偄偔偮丅
丒丒侽丏俁俁俁俁俁俁俁丒丒丒偱偡丅
侽丏俁俁俁俁俁俁俁俁丒丒丒亊俁偼
丒丒侽丏俋俋俋俋俋俋俋丒丒丒偱偡丅
俁暘偺侾偺俁攞偼丅
丒丒偁傟丄侾偩丅侽丏俋俋俋俋ゥ蜄{摉偵侾側傫偐側偁丅
栚師傊