ベイズの定理からベイジアンネットワークへ
知識の創造と活用
モノは二人で分けると1/2になるけど、知識は二人で分けると2倍になる。
この意味で、私たちは投稿や写真などのコンテンツを生み出す「生産者」である。 が、そのコンテンツは利用されている。 例えば、どんな人がどのコンテンツを好むのかとかも個人データの中に含まれる。 FBはこういったコンテンツをどういう順番で表示するのかというアルゴリズムを作っている。 興味を引くものを優先しないと利用者が減るので、例えば10代の少女に心理的な悪影響が出るようなアルゴリズムを知っていて作っていたという。 また個人の好みのコンテンツを選挙の投票に利用するということも行われている。
問題はこういったことを私たちが自覚し、巨大IT企業に規制をかけられるかだ。 欧米ではそういった機運が高まり、実際に自主規制をしたり新たな法律ができているという。
『人工知能と21世紀の資本主義』本山美彦著を読んでいる。
読み始めたときは業界用語が多くて理解できなかったけど、少しずつ読めるようになってきた。
すると、ビックデータの処理の原理のところで、ベイズの定理を用いているところが気になってしまった。
(ところでベイズの定理って何だったけ?)
このデータ処理の一つをベイジアンネットワークといい『条件付き確率(ベイズの定理)』でネットワークの重みを設定することができる。
その時のデータの因果関係を分析するために、
「因果関係の強さを、ある事象が起こった場合に、他の事象が起きる確率である『条件付き確率』の大きさから判断し、多数の事象間の因果関係をグラフで整理する。」
というアイディア。
(こう書いてあるけど具体的なイメージが持てないぞ。)
まずはこのネットワークのイメージを持つための動画。
(でも、これでわかるわけではない。あくまでイメージのみ。
それにしてもこのビデオの表現の仕方は、どうやっているのだろうか?)
このネットワークをつくる「ベイズの定理」とは何だろう? ⇒【数学 と 心理学 〜ベイズの定理の理解の仕方〜】
【例題】(この問題の特徴は、原因(ガン)→結果(陽性)の逆の確率を求めることにある。 つまり結果(陽性)から原因の確率を求めるのだ。 今までこのことを意識しなかったけど、これを書いてよくやく意識できるようになってきた。) ベイズの定理を使うと確率は、0.01×0.9÷(0.01×0.9+0.99×0.09)=0.0917…と求まる。
40歳の女性が乳がんにかかる確率は1%。
また、乳がん患者がX線検査で陽性になる確率は90%である。
乳がんではなかったとして、それでも検査結果が陽性になる確率は9%である。
さて、あなたの検査結果が陽性と出た場合、実際に乳がんである確率は?
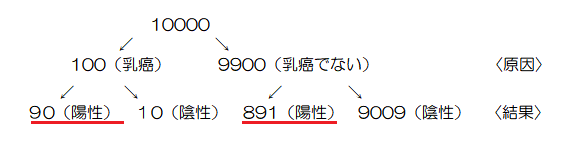
よって、陽性のうちがんである条件付き確率は、90÷(90+891)=0.091・・・
陽性であってもがんである確率は9.2%ほど。90%はがんでない可能性がある。(がんではないけど陽性になる数を忘れていはいけない。)
ここで「陽性の90」を一度に計算するには、1%の90%だから、かけ算で求めることができ、0.01×0.9=0.009と一度に計算できる。
(これが乗法定理だな。)
(何だかあっけないほど簡単に導くことができるな。でも、この式は何を示しているんだろう?)
今度は複数の場合。
【例題】
3つの袋があり、次のように赤い玉と白い玉が入っています。
袋1:赤い玉4つ、白い玉1つ
袋2:赤い玉3つ、白い玉3つ
袋3:赤い玉2つ、白い玉4つ
いずれかの袋から玉を1つ取り出したところ、白い玉でした。
この玉が袋2から取り出された確率はいくらでしょうか?
(この問題は今までの原因・結果という見方を使うと、結果が白玉であったことからどの袋から取り出したのかという原因の確率求める問題だ。)
自然頻度を用いて解いてみる。まず、袋の玉の数を同じにする。
5個と6個と6個だからそれぞれ30個にすると、白玉はそれぞれ6個、15個、20個となり、合わせて41個。
袋2は15個だから、袋2である確率は15÷41≒0.366と求まる。
これを確率で表すと次の図になる。
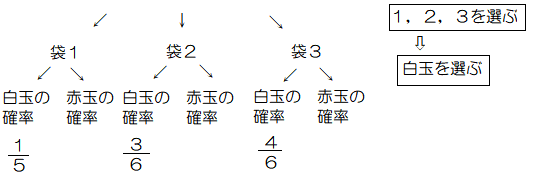
この場合のベイズの定理の意味は、
[白玉が選ばれた条件で袋2から取り出された確率]=
[袋2を選んで白玉が出る確率]÷([袋1を選んで白玉が出る確率]+[袋2を選んで白玉が出る確率]+[袋3を選んで白玉が出る確率])
ということだ。
でも、ベイズの定理に当てはめるよりも自然頻度で解いた方がはるかに簡単。では、この定理の本当の応用はどこにあるのだろうか?
X=(袋2を引く),Y=(白を引く)とすると、P(Y|X)からP(X|Y)を求めたことになる。
先のベイズの定理の導き方もP(Y|X)をP(X|Y)に変えただけだが、
これはXという条件の下でYが起きる確率と、Yという条件の下でXが起きる確率だから、
X(原因)→Y(結果)を、Y(結果)→X(原因)と逆転させることになる。
その意味についてとても分かりやすい説明がこれ。
このビックデータの解析へ通じる道を探り当てたのはジューディア・パールで、 人間の知識は狭く、それを補うために統計・確率的な考え方を人工知能に導入すれば、何度も推論をやり直して前よりも高い確率で現実世界に接近できるのではないかと発想し、 ベイジアンネットワークを立ち上げたという。 ただこれはあくまで過去のデータであって、そのまま未来の予測ができるわけではない。そしてここに結果から原因となる確率を求める「ベイズの定理」が使われる。
このモデルはどういう性質を持っているのか?
そのために単純なモデルを考える。
P(x,y)=P(x∩y) (例えばxが男子であってyがA型のようなもの)
ノードの間の関係。「観測される」というデータをどう用いるのか。
このサイトには、ベイジアンネットワークの機械学習などへの発展が示されている。
ところで、先の本の中に紹介されていたアラン・ケイ氏のインタビューがとても印象的で、IT(もちろんAIも)と教育の関連を考えるヒントがある。
■ アラン・ケイ氏インタビュー■ 「餌を見ることができないで飢死するカエル」の例えは心に残る。