意味のニューラルネットワーク(NN)
「表現」と「推論」と「発見」は分けることができない
1、NNは脳のネットワークの模倣である
そもそも、全ての知はネットワークであり、その模倣が脳のネットワークであると考えれば、知識は相互結合型NNであるはず。
とすると、次の方向が見えてくる。
(1) できるだけこのNNを描く(表現)。それを描くことが推論の一部である。
(2) 描いているうちに新しいつながりが見えてくる(発見)。
(3) するとそれが妥当かどうか考える(推論)。
今回この意味NN(意味宇宙の地図)を描きながら、発見したことをまとめてみよう。
それは、こういう意味NNを描くことの効果(発見のツール)を示したいためと、AIに対抗するためである。
また、表現し推論し発見するためには私たちの感情が欠かせないことを示すためである。
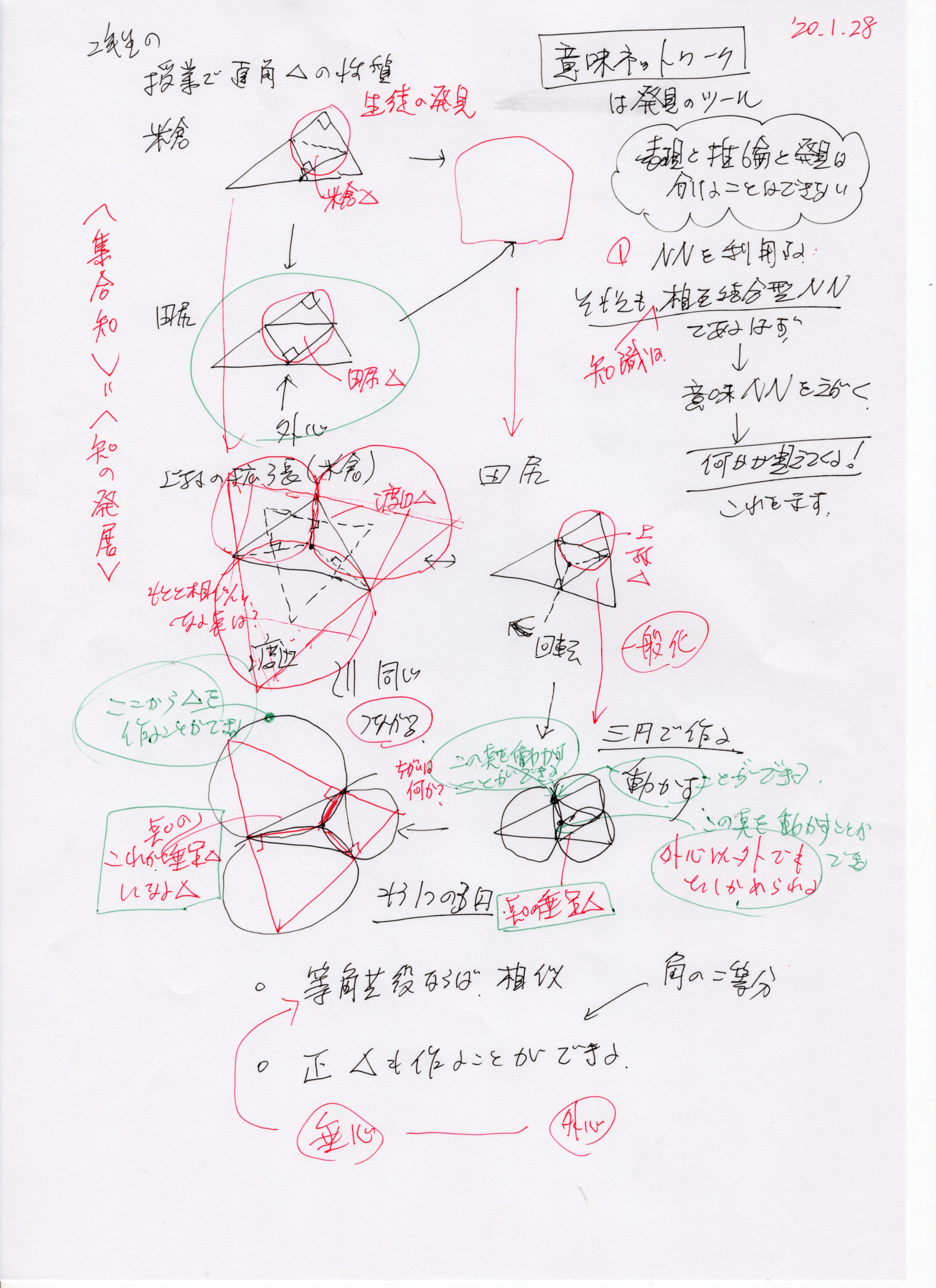
2、生徒の発見した定理
学校で2年生の数学を教えていた時に、米倉さんという生徒が直角三角形の性質で新発見をした。
斜辺の中点に折り曲げれば相似になるということを。さっそく本当かどうか確かめてみた。
二年生には難しかったけど、内接四角形を使えば証明は簡単だった。
数年後それを授業でとり上げたら、田尻君が新発見をした。それは中点に直角をあてて作図すれば相似になるというものだった。
これも内接円を描けば簡単に証明できる(この内接円がポイント)。
この時初めて中点の意味が気になった。
そして、もし直角三角形でなかったらどうなるのだろうと考えてみた。
無意識のうちに一般化を始めたのだ。そしてその点が外心であることがわかった。
外心に折り曲げると相似になるのである。今度は証明にはどんな内接円を描けば良いのだろうか。
このことを別のクラスの授業で話したら、渡辺君が新しい見方を示してくれて、折り曲げた所を延長して三角形を作った。
外心は新しい三角形の内心になっていることにびっくり。
でもこの三角形は相似ではない。この時、外心ではなく他の心を考えればよかったけど、思い至らなかった。
米倉さんの発見は一般の三角形に拡張することができたので、渡辺君のもできるのではないかといろいろやってみたけどうまくいかなかった。
3、拡張するという指向
次は田尻の定理の拡張である。これは外心が中心だということはわかったけど、そこから三角形をどう作図すれば良いのか悩んだ。
いろいろ試していて、垂足三角形を作図すれば良いことに気がついた。点Eを動かすと相似三角形が拡大する。
すぐ気がつくのはAKBNは同一円周上にある。だからこの時、3円から相似三角形が作図できる。それに気がついたのはそれから何十年も後のことだった。
昨年から3円相似の問題に取り組んでいた。
というのは、これらの定理は内接四角形が3つ描け、「田尻の定理の拡張」のように回転させなくても辺上の点を移動させることによって、回転させることができるからだ。
つまり、田尻の定理は自然に3円相似に拡張できる。
このことを説明したのがこのシート。これだと心が決まれば、3円で相似三角形を自由に作ることができる。辺上の点を動かしてみよう。
ところが、3円相似には外と内がある。これが気になって、今までのことを意味NN(最初の図)に描いてみた。
そしてこの二つの作図の仕方の違い(特に外三円の意味)は何だろうかと考えていたら、内の方が田尻の定理(これは年末からわかっていた)、外の方が渡辺の定理と結びついているのではというアイディアが浮かんできた。
このアイディアは、外三円の意味を指し示すと同時に、渡辺の定理でどういう点だったら相似になるのかと考えることができる。
つまり、三円相似ではこの中心を自由に変えることができる。例えば垂心だったら渡辺の三角形が元の三角形と相似になる。
数十年たってこの3つの発見が結びついたのだ。
うれしかったので、ジオジェブラでアプレット(上図)を作ってみた。
(ここで垂足三角形というのはある点からの垂線の足を結んだ三角形のこと)
△ABCから外側に、△ABCが心の垂足三角形になる新しい三角形EFGができる。内側には茶色の垂足三角形ができる。
内側が田尻の定理、外側が渡辺の定理(彼は頂点を折り曲げたけど同じこと)。
このことから、折り曲げてできる三角形とある点からの垂足三角形は対称的であり(垂足三角形と逆垂足三角形の関係)、
外三円の作る三角形は△ABCを垂足三角形にする三角形を作ることだということがわかる。
当時二人とも外心で作図したのだけど、ここでは垂心にしてその違いと意味を探ってみた。
実は垂心と外心は等角共役である。
そして、△ABCの垂心は内三円では内心になり、外三円では外心になる。
この3心の関係は最初の心が変わっても保たれる。
それはなぜなのかが不思議だ。 ⇒ 【内心と外心と垂心が互いに入れ替わる】
このように内三円と外三円の間にはきれいな対称性がある。
4、つながっていくことの面白さ
これで3人のやったことがつながり、併せて新しい課題を見つけ出す集合知の在りかたや発展の仕方、意味の発見とはつながりの発見であることが見えてきた。
そもそもなぜこれにこだわったのかというと、3人の記憶が鮮明だからだ。米倉さんの場合は新発見かどうか様々な人に尋ねた。
そういう思い入れがあるから、その意味を探ろうとしたのだろう。
・垂心で外三円の三角形と外心で内三円の三角形は相似である。 ⇒ 逆中点三角形と傍心三角形
・つまり等角共役ならば相似。 ⇒ 等角共役点について ⇒ 等角共役点では内と外が互いに相似
これを定理の形で書けば、「三角形のある点の作る垂足三角形とその等角共役点の作る逆垂足三角形は相似である」となる。
だけど、こうやってまとめると面白くなくなる。具体的な現象の方がはるかに面白いし楽しい。だって多様だから。
ちなみに外心が作る垂足三角形が元の三角形と相似になるのは中点三角形だから。(これも面白くないな)
・三円で正三角形も作図することもできる。 ⇒ 三角形に内接・外接する三角形の作図(フェルマー点と等力点との出会い)
こうやって表現してみると、「表現」と「推論」と「発見」は分けることができないと感じる。
それは別々の「表現」ではなく、別々の「発見」ではなく、別々の「推論」ではない。
1つの物語なのだ。 ⇒ 「シューベルトが生み出しえた音楽は決して聞けないけど」
目次へもどる
