対立(紛争)解決としての証明の授業
・・・「OECDの学力観 キー・コンピテンシー」から・・・
先日、中2で「二等辺三角形の底角が等しいことを証明する」研究授業があった。三角形の合同条件を使って、二等辺三角形を二つの三角形に分けて底角の合同を証明するという課題である。生徒も熱心に取り組み、課題も練られたものであった。その後の研究会でもいろいろ考えさせられた。
この場合、二等辺三角形を二つに分けるということが、すでに仮定を持っているため、それを自覚できない生徒にとって、かなり難しい課題となっている。さらに、当たり前と思われることをなぜ説明しなければならないのかがわからないから、何をやったらいいのか迷っている生徒もいた。
教科書では三角形の合同条件は証明なしで与えられたものだし、突然それを使って証明するという課題を与えられても、何をわかりきったことをするのかわからなくなる。ユークリッドの証明【命題5】を調べてみると、かなり複雑なものである。生徒諸君は人類史の上でもかなり高度なことをやっているのだ。
1、ユークリッドの発見は「仮説の発見」であった
そもそも、ユークリッド幾何学とは何だったのか。私たちはそれを証明と考える。そして、証明は論証力をつけることと考えている。私は、ユークリッド幾何学とは「仮説の積み重ね」であるととらえたい。
○補助線も仮説
幾何の問題の面白さは補助線の発見にある。では、補助線とは何か。思考の補助ではない。
「もし、ここにこう仮定した線を入れたなら、」という仮定なのだ。つまり、仮説を設定するといってもよい。
○背理法も仮説
ユークリッドの証明法には、命題の早い段階で背理法が用いられている。
背理法も仮説である。もし~と仮定すれば、矛盾が出てくる。よってその仮定は否定される。
この背理法を中学生にも教えたい。
○定義も仮説
こうやって考えていくと、定義も全て仮説であることに気がつく。
「二辺の等しい三角形を二等辺三角形と名づければ・・・」
命題において定義は仮定に含まれる。ただ、この仮定は、与えられたもので、補助線とは少し違う。
でも、定義も自分自身で作っていいのだということを早い段階で教えたい。
私たちは子どもの頃、田んぼで三角ベースをやった。その場その場でルールを作った。これは、公理や定義を自分達で創っていたことに等しい。現在のスポーツ少年団では、ルールは大人が与えたものになってしまっている。
非ユークリッド幾何学が現れてからは、公理も仮説であって、違う公理を設定すれば違う世界が現れてくるということになった。そもそも、非ユークリッド幾何学の誕生は、平行線の公理(公準)を背理法によって矛盾を見つけ出すことで証明することであった。でも、矛盾は見つからなかった。
さて、こういう考えは歴史的には「後付け」であるが、もし、図形の学習に意味があるとしたら、やはり、この仮説設定法にならざるをえない。そして、仮説を進めるには論理が必要となってくる。
2、証明は学力(=コミュニケーション能力)を育てるか
仮説を作り出すことがユークリッド幾何の重要なテーマであると言ってきたが、現場の教科書や授業では、証明することが重視されている。
さらに最近は、コミュニケーション能力が強調され、証明が説明力をつけるスキルであるかのように理解されている節もある。さらに受験対策として、証明のスキルを学ぶことに重点がおかれてしまう。
かってドリル学習が子どもの学力をつけると言われたが、ここでは、スキル学習が子どもの学力をつけることになってきている。
そうすると、学力とは何かを定義しないと先に進めないことになる。では、学力を定義することができるのか。
そもそも、学力を高めようとしているのに、学力についての定義は様々に「分裂」している。
3、学力の定義
学力を明確に定義したという意味で評価されるのが、OECD(経済協力開発機構)の「キー・コンピテンシー(主要能力)」と、そこから導かれた「PISA(生徒の学習到達度調査)型学力観」である。この「主要能力」は単なる知識や技能だけではなく、特定の文脈の中で複雑な要求に対応することができる力である。しかも、この能力が必要だという目的を最初に述べている。
(1) 自立的に行動する能力
(2) 社会的な異質の集団における交流能力
(3) 社会的・文化的・技術的ツールを相互作用的に活用する能力
実は、PISAの学力調査を見ると、日本の学力は年々後退している。そして、文科省は、この状態を学力低下として「ゆとり教育」を撤回した。しかし、学力についての定義を明確にしない状態では、この傾向は続くと思われる。
さて、その文科省のサイトからこのキー・コンピテンシーを調べてみよう。
○PISA型学力観 (3つのキー・コンピテンシーの定義)
------------------------------------------------------------
《科学的リテラシー》
(1) 疑問を認識し,新しい知識を獲得し,科学的な事象を説明し,科学が関連する諸問題について証拠に基づいた結論を導き出すための科学的知識とその活用。
(2) 科学の特徴的な諸側面を人間の知識と探究の一形態として理解すること。
(3) 科学とテクノロジーが我々の物質的,知的,文化的環境をいかに形作っているかを認識すること。
(4) 思慮深い一市民として,科学的な考えを持ち,科学が関連する諸問題に,自ら進んで関わること。
《数学的リテラシー》
「数学的リテラシーとは、数学が世界で果たす役割を見つけ、理解し、現在及び将来の個人の生活、職業生活、友人や家族や親族の社会生活、建設的で関心をもった思慮深い市民としての生活において確実な数学的根拠にもとづき判断を行い、数学に携わる能力である。」
《読解力》
「自らの目標を達成し,自らの知識と可能性を発達させ,効果的に社会に参加するために,書かれたテキストを理解し,利用し,熟考する能力」
------------------------------------------------------------
ここで学力として強調されているのは、社会に参加し、生活をしていく中で発揮される能力である。だから、学力としてコミュニケーションスキルを重視している。単なる知識や技能を高めることではない。現実世界の問題をとらえ、分析し、考えを生み出し、表現していく「ちから」が学力なのである。
私は、学力は共同の関係性の中で成り立つもので、競争の中では学力は低下するものだと考えているが、ここでは「対立(紛争)を解決する能力」を取り上げてみたい。
------------------------------------------------------------
☆対立を処理し、解決し、対立する利害を調整し、または許容しうる解決策をみつけだす能力。
個人が争いを処理し解決する積極的な役割を担うために、以下の能力が必要になる。
(1) 異なる立場があることを知り、現状の課題と危機にさらされている利害について、争いの原因と理由を分析する。
(2) 合意できる領域とできない領域を確認する。
(3) 問題を再構成する。
(4) 進んで妥協できる部分とその条件を決めながら、要求と目標の優先順位をつける。
------------------------------------------------------------
グローバルな現代社会で異質な人々との共存を考えると、この視点ははずせないものなのだろう。
4、授業の中にも対立がある
○わかったわからないという分裂と対立
さて、この対立とは、グローバルなものだけではない。実は授業の中でも起きているのだ。まず、問題や説明がなされた時、わからない、わかったという分裂が生じる。
この分裂を対立ととらえ、その対立を統合し解決していくことが授業であるととらえた時、対立を解決する能力が求められる。毎日の授業では、「わかる」「わからない」の対立をどう解決するのかが常に求められているのではないだろうか。
そして、授業の中で分裂が起きたときに、説明が必要となり、証明が必要となる。元々証明は説得法だったのだ。
知識だけの学力は私的に所有されるものとなってしまう。そして、それは消費されるモノとなる。消費されるものだから売り買いができる。そして、学力は個人のものとなってしまう。
それに対して、学力は共同のものであるという立場から、どういう学びを具体的に提起していくのか。最初に取り上げた二等辺三角形の証明の授業で試みてみよう。
5、授業を編集する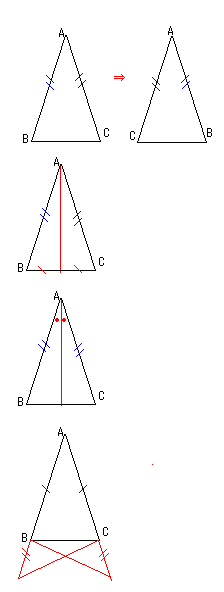
(1)目的
ターレスの定理を証明するためには、二等辺三角形の底角が等しいということを用いる。
辺が等しければ角が等しくなるのだろうか。
(2)定義
二等辺三角形の定義は辺が等しいことである。
(3)証明のみちすじ
・長さが等しいことから角度が等しいことを導く。
・角が等しいことを証明するには、三角形に分けて合同を証明するという「回り道」がある。
(4)証明の方法
では、どんな二つの三角形を考えればいいのか考えてみよう。(全員で)
(5)やり方(どんな二つの三角形を比べたらいいのか?)
ⅰ)裏返した二つの三角形。ⅱ)中線をひく。ⅲ)頂角の二等分線を引く。ⅳ)ユークリッドの同じように辺を延長する。
(以上4種類が考えられる。) その他 ⅴ)垂直二等分線(これはできないが出てくる可能性はある)
(6)やり方を選ぶ(もしⅰを使うとしたら・・・)
どれを使って証明するのかを決めよう。(挙手で確認)
できたら別の方法でやってみよう。
最低1つは証明してみよう。(原則は個人で取り組むが、自由交流も兼ねる。)
(7)確認
それぞれどの方法でできたのかの確認。
できなかった人の立場も聞く。この方法で取り組んだけどできなかった。
どこまでやってみたのか、どこでわからなくなったのかを聞く。
この立場の人たちを(ⅵ)として(8)の説明で突っ込んでもらう。
(8)交流
自分のやった方法を説明してみよう。どう違うのか別の方法を聞いてみよう。(全員で)
(9)納得
どの方法が一番納得できたか。または、納得できなかったか。
ここで、重要なのは(7)であることはお分かりいただけると思う。そして、分裂したクラスの集団に再統一を目指した取り組みが(8)となる。時には「問題を再構成する」必要も出てくる。
(5)はかなり具体的に方法まで示しているが、子どもたちから出なかったら教師の方から示す。そして、板書して空欄を空けておく。(8)でそこに書き込むためである。
(6)は時間をとるが、できた子には板書してもらう時間も含まれる。どれを選んだらいいのかわからない子もいる。その子の所へは真っ先に駆けつける。
6、仲間認識を授業でどう生かすか
《具体的な授業での姿》
課題「0.3χ+0.2=0.5χ+0.4 を解こう」に取り組んでいる時に、どのように解いていったらいいのかという場面で学習集団(クラス)が4つに別れた。
A:両辺を10倍して解く B:そのまま解く C:わからない D:やる気がない
さらに,Bの生徒でもそのまま計算して最後に10倍する生徒がいる。また,ABには計算間違いをする生徒もいる。つまり,問題を提示したときに学級は何層にも分裂している。そうすると,その分裂した学習集団を再統一する視点が必要となる。それが,「仲間認識」なのだ。
このときに,どの階層が良いとか悪いとかいうのではなく,それぞれにアイデンティティを認めながら,さらに学習集団としての統一をめざす。この場合だと,教師の発問は,「どのやり方がいいのか?」ではなく「これらのやり方はどう違うのか?」という発問になる。
「どのやり方がいいのか」という発問は生徒のやり方に優劣をつける。「どう違うのか」という発問は,自己認識を促すためのものだ。そして,CやDの生徒にも参加を促す。
この場合,「結局みんなのやっていることは同じことだ!」という発言が分裂した学級を再統一する視点になると思う。10倍することは計算を簡単にするためで,そのままやっても同じだし,できるだけ簡単になるように計算することでは同じだなと考えていけばいいわけだ。
このように全ての子が学んでいるととらえると,それぞれの学びの質が問われるが,先ほどの例でいうとABCDそれぞれへの指導が必要となる。その場合,TTや生徒のリーダー(ガイド)は大きな力を発揮する。
あるとき,説明をするように指名された生徒が,黒板の前に立ちながら突然,「僕は説明が下手なんだ。」と話し始めた。
「頭の中ではわかっているんだけれど,説明しだすとみんなにうまく説明できないんだ。それで,いつも先生から付け足されるんだ。」
最初,何を言おうとしているのかわからなかったが,彼が言いたかったのは今まで説明で自分が傷ついてきたということだったのだ。
この発言はクラスの生徒たちに大きな影響を与えた。数学ができると思っていたK君がこんな悩みを持っていてそれを突然言い出したのだから。
「今の話わかった?」と聞くと、「わかる。」という。
説明をしたけどもうまくできずに,誰かに補足してもらって傷ついた経験は誰でも持っている。
「K君からこんな告白を聞くとは思っていなかった。説明することも傷つくことがあるよね。だから,それを学べたということはすごいことだと思う。K君もよく言ったと思う。そういう説明だということをこれから大事にしていこうよ。」
うまくいえなかったが,「友だちの発見」が確実にあったと思う。
私自身、納得のいかないことを調べてリライトしている。自分自身の納得の仕方を追求している。それは、きっと他の人へも通じるのではないか。その素材が生活を豊かにし、学ぶことが発見をもたらし、人々をつなぎ合わせることになるはずだ。
そして、一人ひとりの納得の仕方があり、それぞれ違う。でも、私の納得の仕方は私の中だけにあるのではない。わかるということは、関係の中にあると感じる。発見したことは誰かに伝えたくなる。
目次へもどる