１６０年前の１２歳の出した問題に挑戦しよう！
岐阜県養老郡養老町高田の田代神社に天保１２年（１８４１年）に作られた算額があります。この算額の中に１１歳、１２歳、１３歳の少年が出した問題が出ています。もちろん彼らは自分でそれを解いたから算額にしたわけです。この問題に挑戦してみましょう。
最初は１２歳の土屋房吉君の問題です。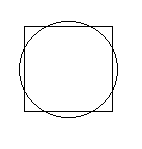
与えられた正方形（一辺が１０寸）に等しい面積を持つ円の直径を求めよ。
答曰（こたえていわく） 円の直径は１１．２寸
術曰（じゅつにいわく） 円の直径＝１．１２×（正方形の一辺）
どうやってこの公式を見つけたのでしょうか？
次は１３歳の井口百一郎君の問題です。
与えられた正方形の中へ四個の等円を入れる。黒い部分の面積を知って、等円の直径を求めよ。
正方形の一辺を１０cm、黒い部分の面積を６０平方cmとすると円の直径はいくら？
答曰 等円の直径は３．５７cm
最後に１１歳の日比野平之丞君の問題です。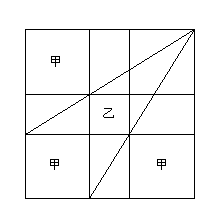
正方形の内に二個の斜線を作り、甲の正方形三個と乙の正方形一個を入れる。甲正方形の一辺の長さを知って乙正方形の一辺の長さを求めよ。
答曰 乙の正方形の一辺＝（√５−１）×（甲正方形の一辺）÷２
ここで注目して欲しいのは，（√５−１）／２が黄金分割ということ。このように正方形を分割すると，辺や斜線も黄金分割されていることがわかる。彼はいったいどうやってこの公式を発見したのだろうか？
さあ、彼等の挑戦を受け取り、さらに君たちも１００年後の後輩達に問題を出してあげようではないか。
参考文献 「岐阜県の算額の解説」 高木重之著