四面体（テトラ）パズル　（四面体になるものを集めました。）

		左のビー玉は接着してあります。 パーツは４つ。 これを組み合わせて右の四面体を作ります。 簡単なようで難しい。
		生協で買ったもの。パーツは６つ。 組み立て方は10種類ぐらいあった。
		プレゼントで頂いた。 ルービックキュブよりは面が少ないだけ易しい。 しかし、構造は難しそうだ。 面の色をそろえる。
		「四八面体」四面体の一種を３部品でつくる。『ＰＵＺＺＬＥ　ＩＮ　ＷＯＯＤ』木のパズル・芦ヶ原伸之著・創和出版より
		左の部品を組み合わせて最も単純な立体を作りなさいと出題するが、なかなかできない。一番最初のパズルと、構造が全く同じことがおわかりでしょうか。
		左の四部品はみな同じ形(四角錐)。これを組み合わせて正四面体を作る。案外難しい。これも、上のパズルをさらに二つに分けたもの。
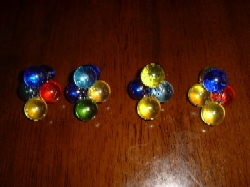		上のパズルをビー玉で作ったもの。バラバラの状態で組み立てようとしてもほとんどできない。２つに組み合わせてから合体する。ヒントは一番最初のパズル。
		100円ショップダイソーで購入。 このパズルはできそうだと思っていたが、ちゃんと作った人がいたのがすごい。上の段の3種類を合わせたパズル。
		動きは、3段より単純だが、形の変化は、より大きい。2段上のパズルと原理は同じで、右上の形にしてねじればテトラになる。 しかし、色をそろえるのが難しい。
		パズルではないが、四面体の利用例。これはクッションだが、その他、牛乳を入れたりして利用されている。
		たためるテトラ。1997年に頴原正美氏が発見。エバラテトラと名づけられる。折りたためられた筒を開くとテトラになる。
		筒型が交差した形は、構造物の接合部に現れる。通常この部分は複雑で強度が強くなければいけないし、固定されている。これをたたんでしまうというアイディアを形にした。たたむことで構造物を手軽に運搬できる。
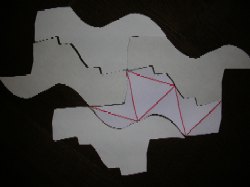
		四面体の4つの頂点を通るように面を切断すると、展開図ができます。この展開図は右と下にあるように二種類の展開があります。さて、この展開図はどんな性質を持っているのでしょうか。 実はこの展開図はしきつめができるのです。
		このことを秋山仁先生から教えてもらいました。面白そうだったのでさっそく作ってみました。なぜ敷き詰められるのでしょうか。右は上の図形を敷き詰めた図形です。エッシャーもこうやって敷き詰め図形を考えたのでしょうか。
		先日の県教研で後藤先生から教えていただいたパズル。この四面体を下の立方体の箱に入れなさい。一見入りそうもないがちゃんと右のように入れることができる。もちろん、四面体をどんな形にしてもぴたりと入る。しかもこう入れると、この四面体とは六面体を二等分したものということがわかる。
		「オスカーズ・ブロック」 ３つの部品を組み立てて右のようにする。これを作るときのほうが面白かった。これは、六面体ではなく四面体の一種と気がついた。
		これはコーヒー用の砂糖の入れ物。 牛乳のテトラはどうなったのだろう。
		１００円ショップで買ってきたボール。投げると右から左へ、左から右へと色が変わる。 よく見ると、これは正四面体である。二つの四面体の面と点を重ね合わせたもの。 ノーベル賞級の作品。

「はまぐりの数学」にもどる