三角形幾何学への誘い
―三角形をめぐる「意味宇宙」の地図―
S:三角形って図形の原子みたいなものでしょう。合同条件以外に何かあるのですか?
T:三角形は単純に見えるけど、実はもっと奥深い意味宇宙があるのです。
S:原子をさらに分けることが出来たように、三角形ももっと分けることができるということ?
T:そうですね。でも、分けるというよりも拡がると言った方が良いかな。
やっているうちにいろいろ興味が出てきて、さらに追求していったらいつの間にやら拡がってしまっていたんです。
そして、調べる手法は「二つのコトの対比」。それは最終的には角度と長さの対比に集約されます。
1、中点三角形
T:まず三角形から新しい三角形を作ることから始めましょう。
S:一番簡単なのが、各辺の中点を結んでできる三角形ですね。
T:これを中点三角形と言います。これを見ているといろいろなことに気がつきます。
S:中点連結の定理で、各辺が平行で相似ですね。
あれ? △ABCの外心Oが△DEFの垂心になっているんじゃないですか?
T:いいところに気がついたね。証明できる?
S:FEは平行だから垂直二等分線は頂点を通る垂線になる。
T:じゃあ、今度は重心はどうなっている?
S:あれ?重心はやっぱり重心か。だって、中線は平行な線をに等分するからね。
T:いいねぇ。今中線という言葉が出て来たけど、この図の点線の線のことですね。
S:とすると、△DEFの中点三角形を作っても重心は変わらないということだ。
S:重心に向かって三角形がどんどん小さくなっていくよ。
T:では今度は、逆に大きくして見よう。
S:△ABCを中点三角形とする三角形を作図しよということですね。やってみよう。(作図)
・・・
S:簡単だ。底辺の平行線を頂点から引けばよい。三つの平行線の交点が新しい三角形の頂点。
T:この三角形を「逆中点三角形」と名づけるよ。さて、それぞれの頂点が中点であることはわかりますか?
S:中点連結定理から当然だけど、不思議に感じるな。
T:逆中点三角形の外心はどこだかわかる?
S:もちろんこの垂心だ!そして、外接円の半径は二倍。重心は変わらない。
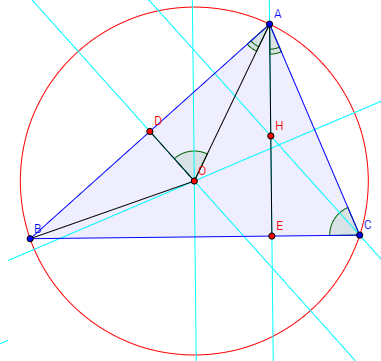
外心が垂心に変わるということは、垂心と外心は何か特別な関係があるような気がするな。
T:いいセンスをもっていますね。では、この図の中に相似な三角形があるんだけど。
S:△AOD∽△ACEだ。OとBを結ぶと中心角ができて、円周角Cの2倍だから、
∠O=∠Cということがわかる。
だから、∠OAD=∠CAEだ。
T:つまり、この角度が等しいということは?
S:外心と垂心は∠Aの二等分線に対して対称になっているということかな。
T:鋭いね。このことはどの頂点に対しても成り立っているから、
外心と垂心は角度に関して兄弟みたいなものということだね。
これは、後から大事なことを指し示してくれます。
そして、この逆中点三角形は次にやる垂足三角形と結びつきます。
⇒【中点三角形をもっと調べたい人の為に】
2、垂足三角形
S:垂足三角形というのは、垂線の足を結んで出来る三角形DEFのことですね。
T:この図を見て何か気がつくことはないだろうか。△ABCの垂心H'は何に変わるの?
S:垂心ではない!もしかしたら内心なの?
T:よく気がついたね。証明出来るかな。
S:直角三角形だから、∠BAE=∠BCF。さらに一つの円周上にあるから円周角の定理を使うと、
∠HDF=∠HDEだ。
T:では、さっきの逆中点三角形と同じように、△ABCを垂足三角形にする三角形を作図してみよう。
S:どうすればいいのかな?・・・さっき、垂心が内心になったんだから、今度は内心を作ればいいんだから・・・
S:つまり、角の二等分線をひけばいいんだ。・・・あれ?これって傍心三角形じゃないの。
T:そうなんです。(鋭角三角形の)逆垂足三角形は傍心三角形ですね。
S:面白いな。逆中点三角形では重心は変わらなかったけど、今度はどうだろうか。
T:今までのことを対比(対)でまとめてみよう。こういう対比をさせていくと、いろいろ予想ができて発見がしやすくなります。
○中点三角形 ○垂足三角形
外心⇒垂心 垂心⇒内心
重心は同じ
○逆中点三角形 ○傍心三角形
辺の中線 角の二等分線
⇒【傍心三角形についてもっと調べたい人の為に】
3、9点円
T:中点と垂足の二つの三角形は別々のように見えるけど、実は共通しているところがある。
S:もしかして、外接円が一致していることじゃないですか。
T:そうです。この中点三角形と垂足三角形の外接円を9点円といいます。
S:どうして「9点」なのですか?
S:まず垂足三角形で3点、中点で3点で計6点。あと3点は?
S:さっき小さな円を作図したよね。この円の中心(垂心と辺との中点)も通るんじゃない?
S:この円の中心は?作図してみよう。(垂心と頂点との中点を作図)
T:これで、外接円と内接円と傍接円と9点円と6つの円が結びついたことになります。
S:9点円の半径は外接円の半分だ。中点三角形を見るとすぐにわかる。
T:9点円は中点三角形と垂足三角形を結びつける大事な円です。
そして、さらにいろいろな面白いことが現れてきます。
⇒【9点円をもっと調べたい人の為に】
⇒【9点円の拡張=垂足円について】
⇒【三角形に関する様々な定理】を知りたい人の為に
T:ここで注目してほしいんだけど、逆中点三角形と傍心三角形を対比すると、
辺の二等分(中点)線(中線)と角の二等分線というように対になっている。
S:垂足三角形から元の三角形を作るには、角の二等分線を引くし、
中点三角形から元の三角形を作るには、辺が2倍になる様に作図していますね。
逆に言えば、角度と長さの半分だ。
T:垂足三角形と中点三角形では浮かんでこなかったけど、傍心三角形と逆中点三角形にすると見えてくる。
S:あれ、垂心とこの9点円の中心と外心は一直線に並んでいるよ。
4、オイラー線
S:重心も同じ線上にある。不思議だな。でも、内心だけ仲間外れだ。
T:点が一直線上に並ぶなんてことはなかなかないことだけど、この4点は一直線上に並ぶ。
この線をオイラー線という。
S:9点円の中心は垂心と外心のちょうど真ん中だ。
S:それに[外心と重心の距離]:[重心と垂心の距離]=1:2じゃないかな。
T:えっ、そうなの?本当?
S:この図を見ると相似だから、重心が1:2に内分しているから当然ですよ。
S:ところで、内心だけ仲間外れだ。内心の仲間はいないの?
T:捜してみましょう。まず、9点円をクリックして、次に内接円をクリック。
するとこの二つの円は一点で接している。その点をフォイエルバッハ点という。
この点と内心を結んでみよう。
S:内心と9点円の中心とフォイエルバッハ点が一直線に並んでいる。
T:さらに、傍接円も描いてみよう。傍接円と9点円も一点で交わる。
この交点と頂点を結ぶとやはり一点で交わる。
S:これも内心の仲間だ。内心は一人ぼっちじゃない。
T:というようにいろんな三角形の心が見つかる。
S:三角形の心って他にもあるの?
T:2015年現在7500以上の心が見つかっているよ。
S:私も発見できるかな。
⇒【オイラー線をもっと調べたい人の為に】
⇒【三角形の心についてもっと知りたい人の為に】
⇒【9点円とオイラー線の研究】
5、キーペルト点と刈屋点
S:一点で交わる3直線ってどうやって探すの?
T:一番簡単なのが三円交線を使う方法。三円交線は必ず一点で交わるからね。
その他、ナポレオンが発見した点とか、フェルマーが使った点とかいろいろあります。
S:日本人の発見した点はあるの?
T:江戸時代の和算家安島直円の発見した「安島・マルハッチの点」というのがあります。
そして、ここで紹介したいのが刈屋点。
刈屋他人次郎氏が1904年に発見した「刈屋点」。
まず、内接円と辺との交点を見つける。この交点と頂点を結んだ時にできる点がジェルゴンヌ点。
刈屋氏はこの点から垂線を立てて、その長さが同じになる様にしたら、やっぱり一点で交わることに気がついた。
S:あれ、これは長さが変わると点が動くよ。
T:そうなんです。では、この刈屋点の軌跡は何を描くんだろうか?
(スライダーをクリックしてカーソルで動かしてみよう)
S:双曲線だ。なぜ双曲線になるんだろう。これ三つの頂点を通っているよ。
S:それに垂心や内心も通っている。
T:なぜ双曲線になるのかはあとで詳しく調べてみよう。では、次にキーペルト点を調べてみましょう。
T:今度は長さではなく角度を同じにします。各辺の二等分線の角度を同じにするんだ。
その頂点とA,B,Cと結ぶと、一点に会する。
これを発見者の名前をとって、キーペルト点という。このキーペルト点の軌跡は?
S:やっぱり双曲線だ。垂心は同じだけど、今度は重心を通っている。
S:なぜ双曲線になるの?不思議だな。
T:刈屋点の軌跡をフォイエルバッハ双曲線といい、キーペルト点の軌跡をキーペルト双曲線といいます。
これらの双曲線は直角双曲線で相似です。
⇒【キーペルト点と刈屋点について】
S:直角双曲線って反比例のグラフですね。
T:そうです。この直角双曲線については面白い性質があります。
6、三角形双曲線
T:直角双曲線上に3点をとって三角形を描きます。この三角形の垂心はどこにあるのでしょうか?
S:垂心も必ず直角双曲線上にありますね。
三角形の頂点つまんで動かすと片方の双曲線に移る。面白いなぁ
S:では、頂点が楕円の上にあったら、垂心も楕円上にあるんですか?
T:このことについては、このブックを見てください。⇒【アポロニウス円錐曲線論】
ついでに、直角双曲線になるわけは次のブックで ⇒【相反共役点について】
三角形双曲線全般についてさらに知りたい人の為に⇒【三角形双曲線】
T:まとめると、三角形の頂点と垂心を通る双曲線は必ず直角双曲線になります。
そして、キーペルト双曲線は垂心Hと重心G、フォイエルバッハ双曲線は垂心Hと内心Iを通ります。
S:あれ?、今度は外心が仲間外れだよ。
T:そうですね。垂心と外心を通る双曲線があるはずだと思いますよね。
そこで、調べてみたんです・・・ちゃんとあるんですね。⇒【ジェラベク双曲線になる直線】
S:三角形には円や直線だけでなく、楕円や双曲線もあるんですね。
S:この双曲線は三角形の心も通っていますね。
さっきのオイラー線などの直線と双曲線とは何か関係があるのでしょうか?
T:そのことを探っていきましょう。
7、等角共役点と等距離共役点
○類似中線と類似重心
T:中線を結ぶと重心が現われます。
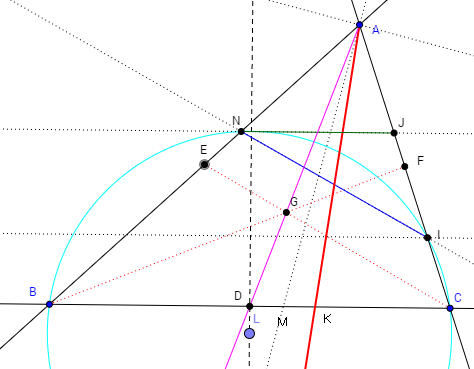
D,E,Fはそれぞれ中点、ADは中線です。中線なので、底辺と平行なNJは二等分に切断します。
中線の右の点線AMは∠Aの二等分線で、赤線AKと中線はこの二等分線で対称になっています。
つまり、∠DAB=∠CAKなのです。
S:さっきの垂心と外心の関係と同じだ。
T:そう、中線ADを角度に対して対称にしたAKを調べてみましょう。
AKはNJは等分していないけど、逆平行(逆の同位角が等しい直線)な線NIは二等分しているのです。
だからAKは類似中線と呼ばれます。
S:ということは類似中線を同様にして3本引けば類似重心が求まるということですね。
T:この重心と類似重心との関係を等角共役点と言います。
S:ということは、垂心と外心は等角共役点ということですね。
⇒【等角共役点についてさらに調べたい人のために】
○等距離共役点
T:今、角度に関して対称な線を引いたけど、中点からの距離を同じにする対称も考えることができます。
実は、どちらの線も一点で交わることが証明できます。これを等距離共役点と言います。
S:角に対して対称の場合が等角で、長さに対して対称の場合が等距離なんですね。
垂心と外心が等角共役点だったような点が等距離共役点でもないのですか?
T:もちろんあります。
有名な点では、ジェルゴンヌ点(内接円と辺との接点を結んだ点)とナゲル点(傍心円と辺との接点を結んだ点)は等距離共役点です。
⇒【等距離共役点についてさらに調べたい人の為に】
8、等角変形と等距変形
T:自由な点Pで、等角共役点P'を作図します。Pをつまんで動かしてみましょう。
等角共役点P'も同時に動きます。何か気がつきますか?
S:Pを真っ直ぐに動かすと、P'は曲線を描きますね。この作図はできますか?
T:いいアイディアですね。今度は直線上に点をとって、等角共役点を作図してみます。
S:その軌跡がどうなるのか見ればいいのですね。・・・
双曲線になりますね。今度は、直接双曲線を描かせることは出来ますか?
T:もちろんできます。5点を通る二次曲線を描けばいいのです。
○オイラー線の等角変形
T:まず、外心を通る直線を作ります。
外心を通るということは、双曲線はその等角共役点である垂心を必ず通ります。
S:直線を動かすことによって、直線と心のつながりがわかります。
T:これを等角変形といいます。
S:この双曲線は垂心Hを通っているので必ず直角双曲線になるのですね。
T:Eを動かして直線がオイラー線(垂心Hを通る)になるようにすると、ジェラベク双曲線になります。
S:Kは何ですか?
T:Kは重心Gの類似重心(重心の等角共役点)です。
これを通る直線は、重心を通るキーペルト双曲線になります。
S:ということは、内心Iと重ねると、内心を通るフォイエルバッハ双曲線になるんですね。
T:そうです。さらに同様のことを等距離共役点で考えると、等距変形が考えられます。
そして、そこから同様に3直角双曲線が生まれます。
S:2つの変形によって、3直線から3双曲線が生まれるのですね。
T:この2つの変形のそれぞれの3双曲線について、きれいな対称性が見つかります。
⇒【3直角双曲線の対称性について】
S:三角形の5心のつながりがわかりました。
そうすると三角形の他の心もこれらの直線と直角双曲線で分類できるような気がします。
T:この三角形の3直線と3直角双曲線とが描く図は、ともて美しいと感じます。
S:中点と垂足点→垂心と外心→キーペルト点と刈屋点→等角と等長(距離)
→等角共役点と等距離共役点→等角変形と等距変形→平行と逆平行・・・
などのように、対称的なものとつながりながら認識がどんどん深まっていく。
三角形って奥深いんですね。
目次へもどる

