奼挘偡傞偐傜偍傕偟傠偄両
乗丂僺僞僑儔僗偺掕棟偺奼挘偺偟偐偨丂乗
丂掕棟丒徹柧丒掕棟丒徹柧丒丒丒偲懕偔悢妛偼側偠傔傑偣傫偱偟偨丅側偤偦偺掕棟偑弌偰偔傞偺偐彂偄偰側偐偭偨偐傜偱偡丅
丂偦偙偱乽徹柧偡傞悢妛乿偵懳偟偰丄乽奼挘偡傞悢妛乿傪懳抲偟傑偟偨丅乽奼挘偡傞悢妛乿偼敪尒傗憂憿傪敽偄傑偡丅怴敪尒偱側偔偰傕嵞敪尒偑偁傝傑偡丅偳偪傜傕婌傃傪惗傒弌偟傑偡丅

丂巹偑悢妛傪傗傠偆偲峫偊傞帪偼丄偙傟傪徹柧偟偰傒傛偆偲偄偆帪偱偼側偔丄偙傟偼奼挘偱偒傞偺偱偼側偄偐偲姶偠偨帪偱偡丅
丂乽傕偟偐偟偨傜偙偆側傞偺偱偼側偄偐乿
丂乽偙偺偙偲偵傕摉偰偼傑傞偺偱偼側偄偐乿
丂乽偙偆偟偨傜偳偆側傞偺偩傠偆乿
丂偙偆偄偆栤偄偐偗傪儅僗僞乕偟偨恖偼丄奼挘偡傞曽朄傪恎偵偮偗偨恖偲尵偭偰傕偄偄偲巚偄傑偡丅奼挘偺拞偵敪尒偺摴嬝傪尒偄偩偡曽朄傪儅僗僞乕偟偰偟傑偊偽丄徹柧傕昁慠揑偵敽偭偰偒傑偡丅
丂偙偙偱丄僺僞僑儔僗偺掕棟偺奼挘傪椺偵偟偰丄悢妛偵偍偗傞奼挘偐傜敪尒偡傞曽朄傪峫偊偰傒傑偡丅
丂乽奼挘偡傞偲偄偆峫偊曽乿偑朙偐側悢妛傪憂傝弌偡偙偲傪懱尡偱偒傞偲巚偄傑偡丅
丂丂乽捈妏嶰妏宍偵偍偄偰丄倎2亖倐2亄們2乿
偙偺桳柤側掕棟傪奼挘偟傑偡丅偳偆偄偆曽岦偵奼挘偡傞偺偐傪弴斣偵峫偊偰偄偒傑偡丅
(1)捈妏嶰妏宍偱丄惓曽宍埲奜偺暿偺宍偱偄偊側偄偐
丂尨宆傪乽偔偢偡乿乽偼偢偡乿乽偢傜偡乿乮儊僞儌儖僼僅乕僛乯偲偄偆敪憐偱偡丅
 仜僸億僋儔僥僗偺掕棟
仜僸億僋儔僥僗偺掕棟
丂僺僞僑儔僗偺掕棟偼丄惓曽宍埲奜偱傕憡帡宍側傜偳傫側宍偱傕惉棫偟傑偡丅傑偢峫偊傞偺偼墌偱偟傚偆丅
丂墌傪昤偄偰傒傑偡丅戝敿墌亖拞敿墌亄彫敿墌丅偱傕丄偙傟偼摉偨傝慜偡偓偰柺敀偔偁傝傑偣傫丅
丂偲偙傠偑丄偙偺恾傪尒偰偄傞偲柺敀偄偙偲偵婥偑偮偒傑偡丅
丂壓偺敿墌傪忋偵帩偭偰偔傞偲丄忋偺敀偄媩宍偺晹暘偼椉曽偵廳側偭偰偄傑偡丅偩偐傜丄偙傟傪憃曽偐傜偲偭偨巆傝偺晹暘傕摍偟偄偙偲偑偡偖偵傢偐傝傑偡丅
丂偮傑傝丄
丂乽墿怓偺擇偮偺寧亖捈妏嶰妏宍乿
丂偙傟偑丄僸億僋儔僥僗偺掕棟偱偡丅
丂偙傟偼丄偲偰傕偒傟偄側掕棟偱偡丅偦偟偰丄墌偺柺愊偑嶰妏宍偵側傞偲偄偆揰偱堄奜惈傕偁傝傑偡丅
仜僷僢僾僗偺掕棟

乽偢傜偡乿
丂墌偺師偼挿曽宍偱偡丅捈妏嶰妏宍側傜惓曽宍傪敿暘偵偟偰傕惉棫偡傞偙偲偑傢偐偭偰偄傑偡丅偱偼丄敿暘傛傝傕傕偭偲彫偝偔偟偨応崌丄懠偺挿曽宍偺斾棪偼偳偆側偭偰偔傞偺偱偟傚偆偐丅
 丂偙偺恾偺傛偆偵俤傪偲傞偲丄摨偠斾棪偺挿曽宍偑帺慠偵偱偒偰僺僞僑儔僗偺掕棟偑惉棫偟傑偡丅
丂偙偺恾偺傛偆偵俤傪偲傞偲丄摨偠斾棪偺挿曽宍偑帺慠偵偱偒偰僺僞僑儔僗偺掕棟偑惉棫偟傑偡丅
丂丂乽悈怓偺暯峴巐曈宍亖擇偮偺僋儕乕儉怓偺暯峴巐曈宍偺榓乿
乽偼偢偡乿
丂偙偺恾傪尒傞偲丄暯峴慄偺摍愊曄姺偱娙扨偵徹柧偱偒傑偡丅偲偡傟偽丄暯峴巐曈宍偵偟偰傕惉棫偡傞偺偱偼側偄偐偲姶偠傑偡丅
丂偦偙偱丄俢傪偢傜偟偰挿曽宍偱偁傞偙偲傪偼偢偟偰傒傑偡丅暯峴巐曈宍偱傕惉棫偟傑偡丅偝傜偵俙傪摦偐偡偲丄捈妏嶰妏宍偱側偔側偭偰偟傑偄傑偡丅偱傕丄忋偺娭學偼惉棫偟偰偄傑偡丅
丂偮傑傝丄堦斒偺嶰妏宍偵傕摉偰偼傑傞偙偲偑傢偐傝傑偡丅偙傟偼丄僺僞僑儔僗偺掕棟偺徹柧偺帪偵巊偆摍愊曄宍傪堦斒壔偟偨傕偺偲偄偊傑偡丅
(2)堦斒偺嶰妏宍偱傕摨偠條側偙偲偑偄偊側偄偐
 仜梋尫掕棟
仜梋尫掕棟
丂師偼乽堦斒壔乿偲偄偆奼挘偱偡丅
丂偮傑傝丄捈妏嶰妏宍傪堦斒偺嶰妏宍偵偟偨傜偳偆側傞偺偩傠偆偲峫偊傑偡丅惓曽宍偱偼惉傝棫偪傑偣傫偑丄堦偮傪挿曽宍偵偡傟偽惉傝棫偮偼偢偱偡丅偳傫側挿曽宍偵側傞偺偱偟傚偆偐丅
丂妏俠偑塻妏偺応崌偲撦妏偺応崌偵暘偗偰挷傋傑偡丅
佱塻妏偺応崌佲
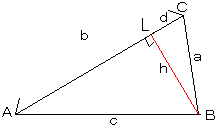
丂曈俙俠偵懳偟偰俛偐傜悅慄傪堷偒傑偡丅倓亖LC丄倛亖BL
丂們2亖乮倐亅倓乯2亄倛2
丂倎2亖倓2亄倛2
丂們2亖乮倐亅倓乯2亄倎2亅倓2
丂丂 亖倎2亄倐2亅俀倐倓
佱撦妏偺応崌佲
丂塃恾丅摨條偵偟偰丄
丂們2亖乮倐亄倓乯2亄倎2亅倓2
丂丂 亖倎2亄倐2亄俀倐倓
丂恾揑側堄枴傕帺慠偱丄乽嶰妏宍偺奺曈偺挿曽宍亄惓曽宍亖惓曽宍乿偲偒傟偄偵昞傢偝傟傑偡丅
丂偦偟偰丄嶰妏娭悢傪巊偆偲堦偮偺幃偵偱偒傑偡丅
丂們2亖倎2亄倐2亅俀倐倓
丂倓亖倎cos俠丂側偺偱丄
丂丂乽們2亖倎2亄倐2亅俀倎倐丒cos俠乿
丂偙偺掕棟偼偲偰傕娙扨偱丄恾宍揑側堄枴傕帺慠偱偡丅
丂偱傕丄挿曽宍偵側傞偲偙傠偑偔偢傟夁偓偱偡丅偁偔傑偱惓曽宍偵側傞傛偆偵偡傞偵偼偳偆偟偨傜偄偄偺偱偟傚偆偐丅
丂梋尫掕棟偼擇偮偁偭偰幃偑懳徧偱偁傞偙偲偵拲栚偟傑偡丅
仜拞慄掕棟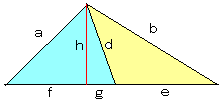
丂嶰妏宍傪擇偮偵傢偗偰梋尫掕棟傪巊偄傑偡丅拞慄傪堷偔偲擇偮偵暘偐傟傑偡丅
丂
丂偦偟偰丄拞慄偱暘偗偨擇偮偺嶰妏宍偵丄梋尫掕棟傪摉偰偼傔傑偡丅
丂丂丂丂倎2亖們2亄倓2亅俀e倗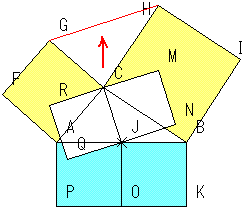
丂丂丂丂倐2亖們2亄倓2亄俀e倗
丂擇偮偺幃傪偨偡偲丄
丂丂倎2亄倐2亖俀乮倕2亄倓2乯
丂乽僋儕乕儉怓偺擇偮偺惓曽宍偺榓亖悈怓偺惓曽宍偲拞慄偺惓曽宍偺榓偺俀攞乿
丂偙偺掕棟偼拞慄偺挿曽宍偑弌偰偒偰丄恾揑偵偼偒傟偄偱偼偁傝傑偣傫丅偲偙傠偑丄恾傪傛偔尒傞偲俻俶傪俧俫偵堏偡偙偲偑偱偒偦偆偱偁傞偙偲偵婥偑偮偒傑偡丅
丂仺俧倕倧俧倕倐倰倎亂奼挘偺僔儏儈儗乕僔儑儞丒丒丒捈妏嶰妏宍偱側偔偰傕僺僞僑儔僗偺掕棟偑惉傝棫偮亃丂亂徹柧亃
仜拞慄掕棟偺奼挘
 丂乽巐暯曽偺掕棟乿偲柤慜傪偮偗傛偆偲巚偭偨偺偱偡偑丄偙傟偼偡偱偵偁傞偺偱巊偊傑偣傫丅
丂乽巐暯曽偺掕棟乿偲柤慜傪偮偗傛偆偲巚偭偨偺偱偡偑丄偙傟偼偡偱偵偁傞偺偱巊偊傑偣傫丅
丂乮儔僌儔儞僕儏偺巐暯曽偺掕棟丅偙偺曽岦傕堦偮偺奼挘偱偡丅乯
丂偲偵偐偔丄拞慄掕棟偐傜傕偭偲恾宍揑側堄枴傪帩偭偨掕棟偑晜偐傃忋偑傝傑偟偨丅帺慠側宍偱係偮偺惓曽宍偑弌偰偒傑偡丅偟偐傕丄偙傟偼偳傫偳傫奼偘偰偄偔偙偲偑偱偒傑偡丅
丂忋偺拞慄掕棟偱丄仮俧俠俫偲仮俻俷俶偑崌摨偱偁傞偙偲偼偡偖偵徹柧偱偒傑偡丅崱搙偼丄擇偮偺惓曽宍傪巐偮崌傢偣偰堦偮偺惓曽宍偵偟傑偡丅
丂傕偆堦偮偺徹柧
丂仮俙俛俠傪俠傪拞怱偵俋侽搙斀帪寁夞傝偵夞揮偝偣傑偡丅
丂偦偆偡傞偲丄仮俵俠俫偑偱偒丄俠俫偼拞慄偵側傝傑偡丅
丂傛偭偰丄拞慄掕棟偑巊偊傑偡丅俧俫亖倓偲偡傟偽丄
丂丂們2亄倓2亖俀乮倎2亄倐2乯
丂乽擇偮偺悈怓偺惓曽宍亖俀亊擇偮偺僋儕乕儉怓偺惓曽宍乿
丂塻妏嶰妏宍偵偮偄偰傕摨條偵偄偊傑偡丅
S丗杮摉偵奼挘偵側偭偰偄傞偺丠
仮俙俛俠傪捈妏嶰妏宍偲偟偰傒傑偟傚偆丅
偦偆偡傞偲丄擇偮偺嶰妏宍偼崌摨偵側傝丄僺僞僑儔僗偺掕棟偑偄偊傑偡丅
偙傟偼丄拞揰掕棟傪傛傝帇妎揑偵偟偨傕偺偱偡丅
嶰妏宍偲惓曽宍偺嶌傞嶰妏宍偺娫偵晄巚媍側娭學偑晜偐傃忋偑傝傑偡丅
丂偙傟傪尒傞偲巐偮偺惓曽宍偑偱偰偔傞偺偱丄嶰妏宍傪偝傜偵巐妏宍偵奼挘偡傞偙偲偑偱偒偦偆側婥偑偟偰偒傑偡丅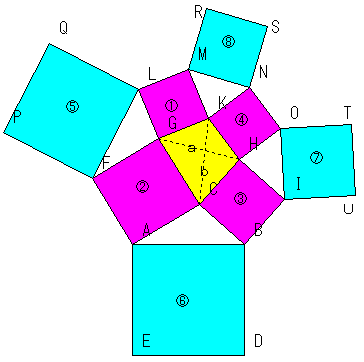
(3)嶰妏宍傪巐妏宍偵偱偒側偄偐
丂巐妏宍偺廃傝偵偦傟偧傟偺曈傪堦曈偲偡傞惓曽宍傪嶌傝傑偡丅偡傞偲丄拞慄掕棟偺奼挘偑巊偊傞偙偲偵婥偑偮偒傑偡丅
仜拞慄掕棟偺奼挘偺奼挘
丂拞慄掕棟偺奼挘傪偦傟偧傟偺嶰妏宍偵偁偰偼傔傞偲丄
丂嘍亄倐2亖俀乮嘇亄嘆乯
丂嘐亄倎2亖俀乮嘇亄嘊乯
丂嘑亄倐2亖俀乮嘊亄嘋乯
丂嘒亄倎2亖俀乮嘆亄嘋乯
丂乽係乮嘆亄嘇亄嘊亄嘋乯
丂亖嘍亄嘐亄嘑亄嘒亄俀乮倎2+倐2乯乿
丂堦斒偺巐妏宍偵偮偄偰傕丄奺曈傪堦曈偲偡傞惓曽宍偺柺愊偺娫偵偼偪傖傫偲偟偨娭學偑偁傞偙偲偑傢偐傝傑偡偹丅
S丗偱傕丄偙偺掕棟偐傜僺僞僑儔僗偺掕棟偑偄偊傞傫偱偡偐丠
丂恀傫拞偺墿怓偄巐妏宍傪挿曽宍偵偡傟偽丄悈怓偺惓曽宍偲倎2偲倐2偼慡偰崌摨偵側傝丄僺儞僋偺惓曽宍傕崌摨偲側偭偰丄係亊乮俀嘆亄俀嘇乯亖俉嘍
丂偟偨偑偭偰丄丂丂嘆亄嘇亖嘍偲側傝傑偡丅
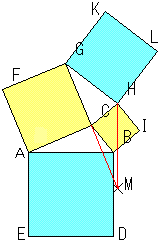
仜僩儗儈乕偺掕棟
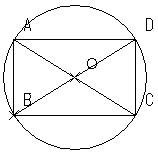 丂墌偺捈宎偼捈妏嶰妏宍傪帺慠偵嶌傝傑偡丅挿曽宍傪嶌傞偲擇偮偺崌摨側捈妏嶰妏宍偑偱偒傑偡丅
丂墌偺捈宎偼捈妏嶰妏宍傪帺慠偵嶌傝傑偡丅挿曽宍傪嶌傞偲擇偮偺崌摨側捈妏嶰妏宍偑偱偒傑偡丅
丂僺僞僑儔僗偺掕棟傪丄懳曈偺愊偲懳妏慄偺愊偵曄偊偰傕惉棫偟傑偡丅
丂偱偼丄挿曽宍傪巐妏宍偵曄壔偝偣傞偲偙偺娭學偼夡傟偰偟傑偆偺偱偟傚偆偐丅
 丂撪愙巐妏宍俙俛俠俢偱丄
丂撪愙巐妏宍俙俛俠俢偱丄
丂俛偐傜俙俠偵佢俙俛俢亖佢俤俛俠偲側傞傛偆偵俤傪偲傝傑偡丅
丂偡傞偲丄憡帡嶰妏宍偑擇偮尒偮偐傝傑偡丅
丂仮俙俛俢佷仮俤俛俠丄仮俙俛俤佷仮俢俛俠丂側偺偱丄
丂丂丂丂丂丂 俙俤丒俛俢亖俙俛丒俠俢
丂丂丂丂亄乯俠俤丒俛俢亖俛俠丒俢俙
丂丂俛俢丒乮俙俤亄俠俤乯亖俙俛丒俠俢亄俢俙丒俛俠
丂傛偭偰丄
丂丂乽俛俢丒俙俠亖俙俛丒俠俢亄俢俙丒俛俠乿
丂側傫偲丄惉傝棫偭偰偟傑偆偺偱偡丅
(4)師尦傪戝偒偔偟偨傜偳偆側傞偐
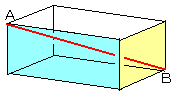 丂俀師尦偐傜俁師尦傊偲奼偘傑偡丅塃恾偵傛傝丄
丂俀師尦偐傜俁師尦傊偲奼偘傑偡丅塃恾偵傛傝丄
丂丂乽懳妏慄偺挿偝亖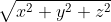 乿
乿
丂偙偺娭學偼丄師尦傪偳傟偩偗奼偘偰傕惉傝棫偪傑偡丅
(5)巜悢傪奼偘傞
丂僼僃儖儅乕偼丄乽倎n亄倐n亖們n乿偺値傪丄俀偐傜俁丄係丒丒丒偲奼偘偰偄偭偨傜偳偆側傞偺偩傠偆偲峫偊傑偟偨丅偦偟偰丄俁埲忋偼惉棫偟側偄偺偱偼側偄偐偲梊憐偟傑偟偨丅
丂乽値偑俁埲忋偺帺慠悢側傜偽丄
丂丂倎n亄倐n亖們n丂偲側傞惍悢倎,倐,們偺慻偼懚嵼偟側偄乿
丂偄傢備傞僼僃儖儅乕偺嵟廔掕棟偱偡丅侾俋俋俆擭偵儚僀儖僘攷巑偑徹柧偟傑偟偨丅
(6)昞尰偺奼挘乮暿偺昞尰乯
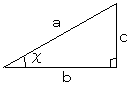 丂暿偺昞傢偟曽偱偡丅椺偊偽丄嶰妏娭悢傪梡偄偰昞傢偡偲偳偆側傞偺偱偟傚偆偐丅
丂暿偺昞傢偟曽偱偡丅椺偊偽丄嶰妏娭悢傪梡偄偰昞傢偡偲偳偆側傞偺偱偟傚偆偐丅
丂僺僞僑儔僗偺掕棟傪巊偆偲丄(c/a)2亄(b/a)2亖(b2亄c2)乛a2亖侾
丂傛偭偰丄
丂丂丂乽sin2倶亄cos2倶亖侾乿
丂偙偙偵偁偘偨偺偼傎傫偺堦椺偱偡丅僺僞僑儔僗偺掕棟偺徹柧偼侾侽侽捠傝埲忋偁傞偲偄傢傟偰偄傑偡丅偲偄偆偙偲偼傑偩懠偺奼挘偺偟偐偨偑偁傞偲偄偆偙偲偱偟傚偆丅
GeoGebra偱摦偐偟側偑傜奼挘偟偰傒傛偆丅偙偙偵弌偰偔傞奼挘偺掕棟偑慡偰弌偰偒傑偡丅佀亂僺僞僑儔僗偺掕棟偺奼挘亃
偝傜偵榓嶼偱傕佀亂愇尨岝塹栧偺栤戣亃
嶲峫暥專
亂僐儅僱僠戝妛悢妛壢乮僸儖儀儖僩嬻娫乯亃
亂嶌恾僜僼僩俧俠倂倝値亃偙偙偱巊偭偨恾偼慡偰偙偺僜僼僩傪巊偭偰嶌恾偟傑偟偨丅摦偐偟偰妋偐傔傜傟傞偟丄柺愊傕媮傔傞偙偲偑偱偒偲偰傕栶棫偪傑偟偨丅
丂丂丂丂丂栚師傊傕偳傞