%F15 【日本の数学】
『数詞の研究』
日本では数の読み方が二つある。[ひ、ふ、み、よ、いつ、む、なな、や、ここの、とお]と、[いち、に、さん、し、ご、ろく、しち、はち、く、じゅう]の読み方である。では、何故2つあるのだろうか。
・・「だるまさんがころんだ」という言い方もあります。
それはかくれんぼに使うね。十の音を十と考えたんだね。でも、ひとつ、ふたつ、という呼び方は今でも使っているでしょう。なぜ、呼び方が二つあるの。
ヒント、日本語の中に漢字が入ってきているのは知っているだろう。
・・あっ、そうか。漢字を読む時
に音読みと訓読みがあるというのと同じでしょう。
では、どっちが訓読み?
・・ひ、ふ、み の方。
ピンポン。こちらの方が、旧日本式読み方。
・・ということは、いち、に、さんは音読みか。
・・ところで、ひとつ、ふたつ、みっつ、と呼ぶ方が正しいのじゃない。
「つ」は年齢を数える時に付ける調子のようなものさ。ひと、ふた、み、よ、と呼ぶのが正式かな。
10までは読めるとして、20は旧日本式読み方ではどうなるの。
・・?
ヒントだよ。20歳のことを古い言い方では?
・・はたち。
だから、20のことを「はた」という。30は「みそ」、「おおみそか」って言うだろう。40は「よそ」、50は「いそ」、60は「むそ」、70は「ななそ」、80は「やそ」、90は「ここのそ」、100は「もも」
・・山口百恵の「もも」か。
500は「いほ」、千は「ち」、八千は「やち」、万は「よろづ」でこれ以上はない。八百万と書いて「やほよろづ」、とてもたくさんという意味だ。
・・億はないの。こりゃ楽でいいや。
11はどう読む。
・・とおひと。
残念でした。「とを」と「ひと」余るから「とをあまりひと」つと読む。「とをまりひと」と略されていた。百三十七は「ももちまりみそなな」。
・・へー。知らなかった。
そうだね。みんなが知らないのは、この読み方が段々すたれてきたからだが、なぜ「じゅういち」という読み方の方になったのかわかるかい。
・・読み方が簡単だからじゃない。
・・十の位もそれぞれ呼び方が違うなんて、めんどくさいよ。「じゅう」さえ知っていれば「にじゅう」、「さんじゅう」、「しじゅう」と読んでいけるもんね。
12は「とをまりふた」「じゅうに」
25は「はたちまりいつ」「にじゅうご」
36は「みそあまりむつ」「さんじゅうろく」
参考文献「数学ウラ話」吉岡修一郎著、学生社。
その他、先生が調べてまだ解らない事が幾つかある。考えてみてください。
(1) この変化の法則は?
ITIHON → IPPON 一本
SANHON → SANBON 三本
ROKUHON → ROPPON 六本
HACHIHON → HAPPON 八本
JHUHON → JIPPON 十本
(2) 八日のことをなぜ「ようか」というのか。
「やか」がなまって「やあか」または「よよか」から「ようか」に変ったのではないか。
4+4=8 よ+よ=や やは大きなよ
3+3=6 み+み=む むは大きなみ
参考文献 『数学ウラ話』寺岡修一郎著
『数学の絵馬と教育の場としての神社、寺』
・・何?これ。数学みたいだけど漢字で書いてある。
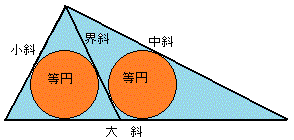
奉懸算題

小斜六十八寸界斜四十零寸問大斜幾何
答曰大斜三百十五寸
術曰置中斜加小斜自乗之而得數之減界斜羃四段平方開之得大斜合問
又有鉤股之内容圓只云鉤… 略
右 神 谷 直 繩
右 宮 川 孟 弼
関流 (越中州、富山之人) 高木充胤門人 某等 敬白
嘉永三庚戌中春
これは、八幡神社(岐阜県郡上郡八幡町小野)に掲げられた算額(さんがく)というものさ。
・・いつ頃のもの?
嘉永三年(1850年ごろ)と書いてあるから150年前の江戸時代ですよ。
・・その頃の人がこんな難しそうな数学をやっていたの。
そうだよ。江戸時代の日本の数学は世界的に見ても相当進んだものだった。しかも、こんな田舎の名もなき人でも数学をやっていたんだよ。
・・うちの先祖かもしれんなあ。数学を誰に教えてもらったんだろう。
やっぱり、先生がいたらしい。ここに、関流越中州富山之人高木充胤門人と書いてあるだろう。
・・富山から教えに来ていたのか。なぜ、神社にこんな額を掲げたの。
当時は神社がコミュニケーションの場だったんだね。神社の社殿が美術館であり、博物館であり、祭の場であり、サロンであったわけだ。自分が、何か面白いことや、新しいことを発見すると額に書いてみんなに見てもらったんじゃないかな。
・・自慢したかったんじゃないの。
それもあるだろうけど、これを見て他の人が刺激を受けてまた新しいことを発見するといったこともあったらしい。数学(この頃の数学のことを和算という)の試合まであったという。
・・進んでいるねえ。
・・進学のために数学をやっていたのとは違うなあ。
ちなみに先の問題で答の出し方は「術曰」の所を訳すと(大=√((中+小)2−4×界2)です。どうやってこの式を求めたのか考えてみてください。わかったらメールをちょうだい。
『160年前の12歳の少年の出した問題に挑戦しよう』
(クリックして印刷して考えてみてください。)
岐阜県に12歳の少年の解いた算額の問題があります。この問題に挑戦してみましょう。ただし平方根について知っていないと解けませんよ。
・・江戸時代に√なんてあったの?
もちろんありました。しかも、12歳の子どもも知っていた。
・・えーっ。信じられん。
『仏教と数学』
徐夜の鐘は幾つつくか知ってますか。
・・108つです。
・・確か、人間には108の煩悩があるから、それを一つ一つ払い去るんだって、教えてもらったよ。
・・煩悩って何なの。
人間の持っている、悩みや苦しみの事ですよ。
・・108もあるの?
ちょっと挙げてみようか。まず、君の悩みは?
・・頭が悪いということ。
・・高校入試が心配。
今は、こればっかりだね。大きくまとめてみよう。昔の人は、人間には四つの苦しみがあると言っている。
まず、死ぬこと。
・・死ぬのはいやだもんね。
次に、病気になること。三つめは老いる事。
・・オバンになるのはいやだ。
最後に、何だと思う。
・・貧乏になること。
・・交通事故で怪我すること。
・・それは、病気に入るよ。
実は、生れることなんだ。この四つを、生老病死と言って四つの苦しみ四苦という。
・・誕生日を祝うのに、生れることが苦しみなんておかしいね。
・・生れることが全ての苦しみの元という事かな。
四苦八苦という言葉を知っているだろう。四苦は説明した通りだけど、八苦というのも有るんだ。まず、愛別離苦。愛し合っているものが別れる苦しみ。二つめは、怨憎会苦。憎しみあっているものが会う苦しみ。三つめは、求不得苦。求めても得られない苦しみ。四つめは、五陰盛苦。殺生、偸盗、邪淫、妄語、飲酒が盛んなこと。
・・後の四つは。
さっきの四苦が合わさるのさ。死による愛しているものが分かれる苦しみ、死によって求めても得られなくなる苦しみ、死によって憎しみあっているものが会う苦しみ、死によって酒を飲む苦しみというように増える。それで、八苦。
・・でも、とても108にはならないな。
四九はいくつ?
・・36。
八九は?
・・72。
36と72で?
・・108。へー。
参考 ----------------------------
六根(目、耳、鼻、舌、身、意)の6感覚
六境(色、声、香、味、触、法)の6対象
三不同(好、平、悪)の3つの受取り方
染、浄の2つの程度
過去、現在、未来の3時
6*3*2*3=108
---------------------------------
T:1−1=は?
S:何もない。
S:無。
S:0。
T:では、この0と10の0は同じですか?
S:同じです。
S:違うよ! 何もない0だとすると、10=1になっちゃうよ。
S:あれ?そうか、10の0は1の位が何もないという事だけじゃなくて、1が十の位にあることを示している。
T:そうですね。10の0は単なる無ではありませんね。1,2という数と同じで、何もないのではなく0という数が有るのです。
まとめると、
(1)
0は5,6世紀頃インドで発見された。人類の最も重要な発見の一つである。
(2)
日本や中国には漢数字があるが、0は使わない。三百を三〇〇と書くのは最近。
(3)
0のおかげで位取り記数法ができた。0が数と認められたおかげで、どんな数でも表わせるようになった。
(4)
この0は、仏教といっしょに東南アジアやアラビアへ伝わった。
(5)
0のおかげで小数が発明された。(小数が簡単にあらわせるようになった)
(6) また、負の数の発見へとつながった。
S:無も数で「有る」と考えたのがインド人のアイディアなのか。
S:どうしてインドで発見されたのですか?
T:それは、インドで起こった仏教(やベーダンタ)の思想からきています。インドでは0のことを「空」といいます。この「空」は仏教の重要な思想です。「色即是空(しきそくぜくう)」という言葉を聞いたことがあるでしょう。では「空」とはなにか。「空」とは、個々の存在はそれ自身として独立に存在するものではなく、ほかのもろもろの存在と無関係には存在しえないということです。
S:わかりません。
T:例えば、みなさんは自分(机でもいいよ)というものが、他に何にもなくてもここにちゃんと存在していると思っているでしょう。空の考え方は、そうではなくて他のものとの関係の上で存在しているのであって、一人で存在しているんじゃないということ。
S:そういう事ならいつもお母さんからいわれている。「一人で生きているんじゃないからね」と。
S:机でいうと、僕たちが使っているから「机」であって、猿から見ると単なる「台」にしか見えないということかな。
S:でも、それがなんで空(から)なの?
T:うん。ここが大事だね。「空」といっても「何もない」ということでなく、むしろ個々の存在と他のもろもろの存在との相依相関の関係をあらわしています。反対に、「空」ではなく「実体が有る」と考えるのは、それが「はじめから他のものとの関係なしで存在している」ということですね。ですから、それを否定すると、「他のものとの関係なしで存在しているのものは無い」となって、これを「空」と名付けたわけです。
S:で、それからどうして0が出て来たの?
T:仏教ではね、空を考えることは、悟り(仏になること)をひらくために必要なことだったんですよ。
S:「悟る」ってどういうこと?
T:「悟る」は「わかる」のもっと深いやつ。問題がでた時、その答えを 知る→分かる→理解する→悟る と深まっていくことを経験したことがない?そして、「悟る」と、本当の自由(解脱)を獲得する。そうすると「本当の幸せ」になる。これが仏になるということ。
S:どうやったら悟れるの?
T:まず「無知」を自覚する。次に欲望(愛欲、生存欲)を順番に克服する。そうすると、「真実の空に達する」ことができ、「悟る」ことができる。つまり、「我」が空であり、「世間は空である」ということがわかることを「悟る」というんだ。このように「空」を考えるインド人だからこそ数字の「空」、つまり0を考え出したのではないかな。
S:うちのばあちゃんが「南無阿弥陀仏と称えると仏になれる」と言っていたよ。
S:おれなんかとっくに悟っている。
S:ぼくは、「分かる」と「悟る」の区別がつかん。
T:大きな数をあらわすとき、「恒河砂」とか「無量大数」という位を知っているでしょう。こういう位を考えだしたのもインド人ですよ。恒河砂(ごうがしゃ)というのはガンジス川の砂の数程の多さという意味です。また、劫(こう)という何億年の時間の単位も考えていますよ。例えば、阿弥陀仏(宝蔵菩薩)は五劫の間、全ての人のために修行をしたんですよ。
S:インド人は、大きなことや夢みたいなことを考えるのが好きなんですね。
T:もともと、瞑想的で空想的なところがあるんですよ。
参考文献 『「大乗起信論」を読む』高崎直道著