月食から月と地球の大きさを求める

― 月食の３．５時間は地球の大きさを示している ―

１、２０１１年１２月１０日の皆既月食

久しぶりに月食を見ました。天気もよくキレイな赤い月を見ることができました。
月をスクリーンに、地球の影が映されるのですから見事な現象です。
でもそれだけではもったいないと思い、【月と地球の大きさ】を求めてみようと考えました。
最初、写真から地球の影を出して大きさの比較をしようと思ったのですが、地球の影は地球の大きさと同じかどうかを考えていて、太陽の視直径を考慮しないといけないことに気がつきました。

１２４、金網の影の逆転現象について・・・太陽の影（２０１１．３）で考察した太陽の視直径です。

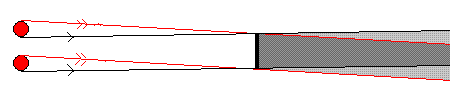
この図は太陽が二つありますが、太陽光線を平行にするための工夫です。
ここでは金網が地球です。
太陽は、はるか彼方にあるので（光は平行とみなせば）影は地球の大きさをそのまま映し出しますが、太陽の視直径があるため本影は小さくなっています。
完全な影の部分と太陽が部分的に隠れている影の部分があります。これを半影食というそうです。
この影の中を月が動いていくのです。
下図の「Ｍｏｏｎ」（橙の点）を影の中に置いてみましょう。下の二つの円が影です。Ｍｏｏｎ２で位置がわかります。

さて、これからの計算は大雑把に行ないます。

２、月は一時間で自分の直径と同じ角度を動く

まず、月の公転角度を求めます。
一月で一回転するわけですから、３６０度÷３０日＝１２度／日＝１２度／２４時間＝０．５度／時間

ところで、月と太陽の視直径は、ほぼ同じで０．５度です。
ということは、月は１時間で月１個分動いていることになります。
一方、地球の公転は３６０÷３６５≒１ですから１時間にすると１／２４°ですから、無視して良いでしょう。
さて、そうすると、影の大きさを時間で測ることができることに気がつきます。
つまり、１時間で月一個分動くわけですから、影を横切るのに３時間かかったら影は月の３倍ということになります。
今回の月食の時間を調べると、次のようでした。⇒【国立天文台暦計算室】

半影食の始め 20h32m
部分食の始め 21h45m
皆既食の始め 23h06m
皆既食の終り 23h58m
部分食の終り 1h18m
半影食の終り 2h32m

ではどこの時間でしょうか。

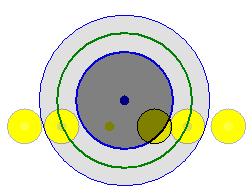半影食の部分は、太陽の視直径と同じですから、月の直径と同じです。
つまり、半影食の時間は１時間のはずです。
ところが、昨夜の結果を見ると、１時間１３分かかっています。
これは差が大きすぎるので、なぜだろうと考えました。
国立天文台暦計算室の図を見ると、月は地球の影の下の方を動いているので、半影食の部分の時間が長くなったと思われます。

（ちなみに、真ん中の影の部分は地球の大きさと同じではありません。
この図の緑色の部分が地球の大きさです。半影と本影の真ん中です。
わけは上の「金網の図」を見てください。）

３、月と地球の大きさの比を月食の時間で求める

そこで、丁度影の真ん中を通過した月食を探してみました。
この【国立天文台暦計算室】には過去の月食のデータも検索できます。
２０１１年の６月１６日の月食がほぼ影の真ん中を通過しています。

半影食の始め 2h23m
部分食の始め 3h23m
皆既食の始め 4h22m
皆既食の終り 6h3m
部分食の終り 7h3m
半影食の終り 8h2m

ほぼ１時間です。
地球と同じ影の大きさは「半影食の始め」から「皆既食の終り」までですが、「部分食の始め」から「部分食の終わり」までと考えても同じです。
時間を求めてみると、６時３分－２時２３分＝３時間４０分
７時３分－３時２３分＝３時間４０分＝３.６６…時間です。
ということは、地球の大きさは月の大きさの３．６６倍ということになります。
この値は実際の値とほぼ一致します。大雑把でも大丈夫なのですね。

今回の月食の時間は３．５時間でした。
この時間が、月と地球の大きさの比を表わしていることがわかった月食でした。

　　　　　目次へもどる