籠目（カゴメ）編みとフラーレン
籠目（カゴメ）編みとフラーレン
― セパタクローからサッカーへ ―
１、セパタクローの作り方
T：今まで正三角形と正方形と正六角形で正多面体を作ってきたね。今日はセパタクローを作ろう。
S：セパタクローって何ですか？
T：東南アジア各地で９世紀ごろから行われている足で行うバレーボールの様な球技だよ。
←そのボールがこれ！！
S：見たことがあるよ。どうやって作るの？
T：荷造りをするクラフトバンドで作るんだ。
この紐巾は1.5cm。長さ３０cmで６本用意しよう。
(1)最初に五本で星型五角形を作ります。
(2)残りの一本を輪にして、星型五角形の外側のヒモを輪の中に入れます。
(3)そして、同じ様に五角形を作るように織り込んでいきます。
(4)６本とも一つの輪になるので、重ねて絞めたらボンドで固定します。
S：これも数学なんですか？
T：もちろん。手でやる数学。
S：できた。蹴鞠をしてみよう。セパタクローのルールも調べよう。
S：五角形が十二あるよ。正十二面体ですね。
S：でも、頂点でつながっているから、少し違うような気がする。
S：サッカーボールのような気もするな。六角形があれば、サッカーボールになるよ。
T：そうか！六角形を入れるとサッカーボールになるね。できそう！！
・・・（五角形の回りを六角形にする）
できた！サッカーボールだ。
２、六角形の籠目編み
S：へー、サッカーボールだ。それにセパタクローよりずいぶん大きくなっている。
S：こっちの方が蹴りやすいよ。
S：これも、サッカーボールと少し違うような気もするな。
S：他の形も作れるのですか？
T：そうだね。何だか作れそうな気がしてきた。考えてみよう。
最初に、六角形だけだと平面になるね。調べてみたら、こういう編み方を「籠目編み」といって、昔から竹で作られる籠などに使われている。さて、五角形はここにある。
S：かどですね。五角形があると曲がります。
S：三角形や四角形はできないのですか？
T：四角形と三角形はつぶれてしまう。でも七角形以上はできるよ。
さて、カゴメ編みで立体を作るにはどうしたらいいのか？
S：この竹細工を見ると、五角形の所で曲がっていますね。
S：五角形がポイントみたい。
３、五角形と六角形
T：もう一度、セパタクローを調べてみよう。
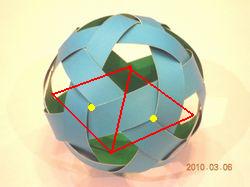
S：三本の格子が交差する点を結ぶと、これは（真ん中）正十二面体になります。
S：こういう（右端）分け方をすると、サッカーボールになるよ。
T：サッカーボールのような正五角形と正六角形でできている多面体を準正多面体（２種類以上の正多角形だけでできた多面体）といいます。正式名称は角切り二十面体。
S：準正多面体ってまだ他にもあるのですか？
T：１４種類あります。
S：籠目編みだと五角形と六角形の２種類しかできないということですね。（正確には七角形も八角形もあります）
S：そうすると、正多面体は正十二面体しかできないな。
S：でも、このサッカーボール（上の黄色のサッカーボール）を見ていると、正二十面体に見えるんだけど。
S：なぜ？
S：この五角形の所が尖っているでしょう。そこを頂点と考えると１２個。六角形の所を面と考えると２０面あるよ。
T：そうだねぇ！ ということはもしかしたら、六角形を増やせば、正二十面体ができるかも。作ってみよう。
・・・
S：まだ作っているんですか？無理じゃないの。
T：難しいな。でも、できそう。とにかく規則通りに作っていく・・・。できた！
S：確かに正二十面体になっていますね。
T：どこに五角形を入れるのかによって、大きさを変えることができます。ちなみに右側は１５本使いました。
≪五角形と六角形の組み合わせで、他の立体ができないか？≫
４、オイラーの多面体定理を使って
T：これまで考えてきたように、カゴメ編みで作った立体は、三本格子の交差点を結ぶと多面体と考えることができます。多面体ならば前にやったオイラーの多面体定理が使えますね。
S：多面体は 点＋面−辺＝２ となるという定理ですね。
T：面は五角形と六角形のみでできている多面体とする。
五角形の数をχ個、六角形の数をｙ個とする。
頂点に集まる面の数は３だから、
頂点の数は、（５χ＋６ｙ）÷３
二つの面で辺ができるので、
辺の数は、（５χ＋６ｙ）÷２
オイラーの定理に当てはめると、
（５χ＋６ｙ）／３＋（χ＋ｙ）−（５χ＋６ｙ）／２＝２
すると、ｙが消えて
χ／６＝２
つまり、χ＝１２
５、五角形の数は必ず１２個になる！
S：不思議ですね。五角形と六角形で立体を作ると、閉曲面なら五角形は必ず１２個必要なんですね。
S：そういえば、サッカーボールも正十二面体も五角形の数は１２個ですね。
S：竹かごは、五角形が６つあると垂直になりますね。これは、閉曲面の半分と考えたら説明がつく。
S：さっき五角形を頂点と考えて、二十面体ができたけど、これも五角形が１２個だから、頂点が１２ということですね。
S：正二十面体と角切り二十面体（サッカーボール）は点と面を入れ替えただけだ。
S：でも、面を頂点とするのはなんかおかしいような気がする。
T：このオイラーの多面体定理の式をよく見ると、点＋面−辺＝２ だから、点と面を入れ替えてもこの式は成り立っている。この場合の様に五角形の面を頂点として頂点を面と考えた多面体を、元の多面体の「双対（そうつい）多面体」というんだ。
S：正二十面体と正十二面体は双対多面体ということですね。でも、面を頂点と考えることはわかったけど、点はどうやって面にできるんですか？
T：面を点と考えて、点を結ぶと面ができる。丁度３面で１つの点があるから、３点で１つの面ができる。１のサッカーボールの左を見るとわかるよ。
S：もしかして、他の形もこれを使って作れるんじゃないですか。
６、五角形を頂点にすると…正四面体・正八面体・正二十面体が！
T：五角形を頂点とし、六角形を面とすると・・・
S：例えば、四面体だと頂点は４つだから、各頂点に３つの五角形を作れば（３×４＝１２）できそうだ。
よし、作ってみよう。
・・・
できた！
S：これは六角形の数を少なくできますね。
S：だんだん少なくしていくと、おにぎりになる。
今まで作ってきた立体を、入れる六角形の数でまとめると
セパタクロー 0
↓ ↓
おにぎり 3 サッカー 20
↓ ↓
たわら 6 正二十面体
↓
正四面体
T：これらはボール以外にも何かに使えないですか？
S：ランプシェードとかに使えそう。
S：花立てにも使えますよ。
S：じゃ次は八面体だ。
S：２個×６点＝１２個
S：２個をどう並べるかで形が違ってきますね。
・・・
とりあえず作ってみました。八面体だけど、正とはいえませんね。（左）
T：これで、四面体・八面体・十二面体・二十面体ができたことになる。
S：でも、正六面体の頂点は８個だから１２個をうまく分けられないね。
S：頂点に五角形を６個集めたらどうなるだろう。
S：六角形の数によって違ってきますね。どんどん六角形を増やしていくと、棒になりますね。
S：カーボンナノチューブみたい。
７、フラーレン
T：実はこの形は重要で、
『フラーレン (fullerene) は、最小の構造が多数の炭素原子で構成されるクラスターの総称である。数十個の数の原子から始まる炭素元素同素体である。1985年に最初に発見されたのは、炭素原子60個で構成されるサッカーボール状の構造を持ったC60フラーレンである。この発見により、ハロルド・クロトー、リチャード・スモーリー、ロバート・カールは、1996年度のノーベル化学賞を受賞した。』
という化学物質の構造を示している。立体構造を持った分子が存在することは驚きで、この中に原子を閉じ込めたりして様々な応用が考えられている。
≪Ｃ60 はサッカーボール。では、Ｃ70 をつくってみよう≫
⇒ 
S：六角形をどんどん増やせば、チューブになるわけか。
S：こうやって作っていくと、フラーレンとカゴメ編みは構造が同じということですね。
８、七角形を入れると
T：今度は七角形や八角形を使って凹や枝のある立体を作ってみよう。
S：ダルマができた。七角形を３つ作ったら、五角形は１５になったよ。
S：七角形が一つ増えると、五角形も一つ増えるんだ。
T：これもオイラーの定理に当てはめてみよう。
七角形の数をｚとするよ。
すると、
(５χ＋６ｙ＋７ｚ)／３＋(χ＋ｙ＋ｚ)−(５χ＋６ｙ＋７ｚ)／２＝２ だから、
χ−ｚ＝１２
S：χ＝１２＋ｚか。やっぱり、七角形が一個増えると五角形も一個増えるね。
S：オイラーの定理ってすごいね。
T：この定理を使うと、こんなものも作れます。
T：６本の突起を作ろうと思っていたら、ミッキーマウスだと言われて方針を転換しました。
S：ミッキーというよりもクマみたい。
T：耳には五角形がそれぞれ６個。七角形は耳のつけ根に３個ずつ、鼻の上に１個。五角形も鼻や首で７個。後ろはちゃんと六角形になっています。
９、五角形は特異点
S：こんな質問をするのは恥ずかしいけど、五角形を作るとなぜとんがるのですか？
T：いやいや、良い質問ですよ。六角形だけで平面になることはわかるけど、五角形でとんがるのはわかりにくいもんね。
さて、このように六角形の平原に五角形を入れると、山ができます。
その火口は五角形で、それまで平行だった稜線は交差します。
ちょうど、強力な重力に曲げられる光のように山によって曲げられます。三方向の平行線が、山の頂上を境に向きを換えているので交差するのです。
S：六角形だけの場合とどうちがうの？
T：右の写真を見てください。山の部分だけちがうのではなく、全体も五角形になっています。六角形の場合は全体が６（三方向）でしたから、全体の構造も変化しているのです。
S：それじゃあ、五角形が増えていくとどうなるんですか？
T：そうだねぇ。一体どういう構造になっているんだろうか。実際に作って調べてみましょう。
T：上の写真は、左から五角形が１個、２個、３個の場合。全体の構造を見ると、五角形→四角形→三角形となっています。
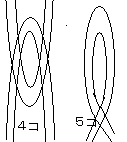S：それから、山で曲がる時、向きがだんだん回転しているのがわかります。
S：じゃあ、４個の時にはどうなるんだろう？
S：ニ角形や一角形になるのかな？
S：いや、付け足すヒモがニ方向になるんだ。(右図→）
S：５個の時は？
S：付け足すヒモの方向が一方向になる。
S：６個では？
S：０方向ということは、付け足すヒモは０本。つまり加えるヒモはいらない。それまでのヒモで六角形を編んでいける。
T：これから作ってみようという人は、これを参考に、編みこむ時もこの原理で編みこんでいけば、自然に編んでいくことができます。
≪追加≫
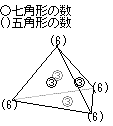
テトラポッドを作りました。頂点から作りはじめました。まるで難しい問題を解いているような気がしましたが、上記のヒモ（テープ）の追加の原則を踏まえて、何とか作ることができました。
最初に設計図を書きます。各面に七角形を３つずつ作ります。
６×４−３×４＝１２
七角形の作る場所を間違えると組み直しです。
１０、七角形の周りは負の曲率になる
S：ところで七角形だとなぜ凹むんだろう？
S：五角形でも逆にすれば凹むよ。
S：じゃあ、五角形と七角形の違いは何なの？
T：六角形の中に五角形を作ったように七角形も作ってみよう。
S：最初に七角形を作ってと・・・別に曲がらないよ。
S：いや、だんだん六角形を増やすにしたがって曲がってくる。
S：全体も七角形になっているよ。
S：七角形の向かい合う辺は狭まっているから、六角形を無理矢理作っていくと空間が広がってくるんだ。
T：そうなんです。七角形のみでは曲がらないけど、周りに六角形を作っていくと空間が曲がってくるのです。
S：馬の鞍のようなのになったよ。
S：凹んでいるんじゃなくてふくらんでいるよ。でも、五角形とはちがう。
S：五角形を二つ作り、一つは表に、一つは裏にすると、凸と凹の面になるけど、七角形は凸凹じゃあなくて、空間がしわくちゃに・・・のびているんだ。
S：でも、まだ五角形の場合と七角形の場合の違いがわからないよ。
T：そのしわくちゃを計算するために半径１の円を描いてみましょう。そして、円周の長さを求めます。
S：平面に描いた場合は、円周がちょうどπですね。
T：そうです。では五角形の場合はどうなるのでしょう。
S：球と同じだから、円周はπよりも短くなります。そうか、しわくちゃということは、七角形の場合は円周がπよりも大きくなる。
T：この円周から空間の曲率という概念が生まれてきます。平面や平面を曲げた曲面は曲率０。球は曲率が正で、鞍は曲率が負と分類できるわけです。
だから、六角形は曲率０、五角形は正の曲率を持っていて、七角形は負の曲率になると言えるわけです。
S：へー。おもしろい。・・・まだ、何かありそう。
１１、トーラスを作る
S：先生、その顔どうしたんですか？
T：やっぱりわかりますか。実は、夕べ一睡もしていないんですよ。
S：また、数学の問題を解いていたの？
T：そうなんだ。解けたのが朝方６時。うれしかった。途中寝ようかと思ったけど、気がついたら４時を回っていたので、そのまま起きていた。
S：一体どんな問題なんですか？
T：それは、これです。（⇒写真）
S：ドーナッツだ。これを作っていたんですか？
T：そうなんです。余ってしまうヒモが出てきて、３回も組み直しましたよ。あきらめかけたけど、方針が見つかったから最後までやろうと思った。全部で９時間もかかってしまった。
S：どうやったらこんな形が造れるのですか。
T：七角形を利用して作れるのではないかと思ったのです。そこで、例によってオイラーの多面体定理に当てはめてみた。
S：あれ、これは８章でやったんじゃないの？
T：いや、ドーナッツ型は球のような閉曲面とはまったく違う性質を持っているから、公式が少し変わります。
ドーナッツのように穴の開いた立体をトーラスといいます。この穴の数を「種数」といって、この面を区別する大切な数なのです。
そして、オイラーの多面体定理は、
点＋面−辺＝２−２×種数
となります。
S：今まで作ってきた立体は、種数が０だから、＝２ なのですか。そうすると、ドーナッツの場合は、種数が１だから、＝０ になりますね。
つまり、
(５χ＋６ｙ＋７ｚ)／３＋(χ＋ｙ＋ｚ)−(５χ＋６ｙ＋７ｚ)／２＝０
χ−ｚ＝０
χ＝ｚ
七角形の数と五角形の数を同じにすれば良いんだ。
T：だから、最初に穴の中に七角形を１０個作った。これはすぐにつながり、輪になった。次は、どこに五角形を作ればいいのかだ。これがわからない。五角形の間隔は等しくしなければいけないけど、試行錯誤。
S：それで、時間がかかったわけだ。
T：あきらめかけた時に、七角形の位置が対称であることに気がついて、その位置に五角形を置いていったら、見事に全てのヒモがつながった。
その時、数学の難問を解いた時と全く同じ気持ちになったよ。
S：五角形の数が裏と表で５個ずつだから、全体として五角形になっているんですね。これ、何かに使えそう。
S：それに、ドーナッツの中を覗ける。
T：「ポアンカレ予想」という、２００３年にロシアの数学者ペレルマンによって証明された、有名な問題があります。
『数学的に厳密ではないが、たとえて言えば、宇宙の中の任意の一点から長いロープを結んだロケットが宇宙を一周して戻ってきて、ロープの両端を引っ張ってロープを全て回収できた場合、宇宙の形は概ね球体（＝ドーナツ型のような穴のある形、ではない）と言えるのか、という問題である。』ウキペディアより。
このカゴメ編みで編んだドーナッツを見ると、なんとなくイメージできますね。
参考文献 【フラーレン・五角形の秘密】
目次へもどる