フラクタルの不思議
― ニュートン法で複素平面を色分けする ―
今から２８年程前にＮ８８ベーシックを使ってニュートン法で複素平面のフラクタル図形を作ったことがある。当時は、一つの画像を描かせるのに一晩かかった。それがこのパソコンだと数分で描ききる。
そのことを思い出しながら、再度計算してみた。プログラムは単純なのだが、できた図形は不思議な景色を描く。その図があまりにも不思議なので、つい拡大したくなる。そうするとフラクタルであることに気がつく。でも、なぜそうなるのかはわからない。
その図形をどうやって作成するのかをまとめてみた。手術で入院中でもあり、少し根を詰めると脈拍数が上がる。資料もなく、思い出すと言うより再度計算することになってしまった。でも、それが結構面白いのだ。
１、方程式の根を見つけるニュートン法
ニュートンは、微分を使って方程式の解を近似的に見つける方法を考え出した。
まず、３次方程式で考えてみよう。
この方程式をｙ＝ｆ(ｘ)とおき、あるｙ＝点a0での接線を引くと、y軸との交点は解にさらに近づくことが予想される。その交点をa1として、さらに繰り返せばやがて解に近づいていく。
これを式で表すと次のようになる。
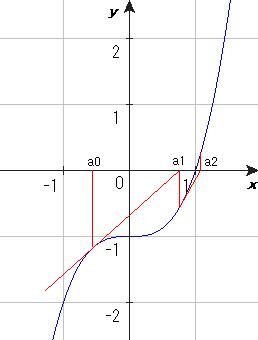ある点aでの接線はｙ＝ｆ'(a)ｘ＋ｂ
よって
ｆ(a0)＝ｆ'(a0)×a＋ｂ
ｂ＝ｆ(a0)−a0ｆ'(a0) よって
ｙ＝ｆ'(a0)ｘ＋ｆ(a0)−a0ｆ'(a0) と接線の方程式が見つかる。
０＝ｆ'(a0)ｘ＋ｆ(a0)−a0ｆ'(a0) から次のa1を求めると、
ｘ＝ａ1＝(aｆ'(a0)−ｆ(a0))／ｆ'(a0)
＝a0−ｆ(a0)／ｆ'(a0) ・・・(1)
a1の値を(1)のa0に代入すれば、a2の値が求まる。これを繰りかえすと、
a0 a1 a2 a3 a4 a5
0.5 1.666666667 1.231111111 1.040670624 1.00156875 1.000002456
このように1に収束していく。
２、複素平面の面白さ
ここでｆ(ｘ)＝ｘ3−1 の解を、ニュートン法で求めてみよう。
ｆ(ｘ)＝ｘ3−1
＝(ｘ−1)(ｘ2＋ｘ＋１)
＝(ｘ−1)(ｘ＋0.5＋i√3／2)(ｘ＋0.5−i√3／2)
ｆ'(ｘ)＝3ｘ2
(1)より
a1＝a0−ｆ(a0)／ｆ'(a0)＝(2a03＋1)／3a02 ・・・(2)
解に複素数があるので、a0は複素平面で考えなくてはいけない。
つまり、ニュートン法を複素平面に拡張する。
そこでa0＝α＋βｉ とおき、(2)に代入する。
(2a03＋1)＝2(α＋βｉ)3＋1＝2(α3−3αβ2)＋1＋2(3α2β−β3)ｉ
3a02＝3(α＋βｉ)2＝3(α2−β2＋2αβｉ)＝3(α2−β2)＋6αβｉ ・・・(3)
ここで、実部と虚部に分けて、
a＝2(α3−3αβ2)＋1
b＝2(3α2β−β3)
c＝3(α2−β2)
d＝6αβ
とすると、(3)から、
a1＝(a＋bi)／(c＋di)＝(a＋bi)(c−di)／(c＋di)(c−di)＝((ac＋bd)＋(bc−ad)i)／(c2−d2)
つまり、
実部α1＝(ac＋bd)／(c2−d2)
虚部β1＝(bc−ad)／(c2−d2)
となり、これを再度繰り返せば、a2＝α2＋β2iが求まる。以下同様に繰返す。
a1 a2 a3 a4 ・・・
α 0.5 0.173333333 -0.938556228 -0.532207122 -0.456986628 -0.498648377 -0.500003624 -0.5
β 1 0.453333333 -0.641886001 -0.668190611 -0.890679302 -0.863977435 -0.866030237 -0.866025404
この値は上の例の様に３つの解のうちのどれかに収束するはずである。
複素平面上点がどこに収束するのかで３色に色分けする。
さらに、遇数回で一定値に収束するか、奇数回で収束するかで濃淡をあらわす。
ここからがパソコンの便利なところである。
a0を(−1＋i)から(−1−i)へ、一点(1ドット)ずつ計算させ、色をつけていく。
ここでは1へ収束する点を緑、0.5＋√3／2iへ収束する点を赤、0.5−√3／2iへ収束する点を青とした。
そして、順に１０倍ずつ拡大していった。５枚目以降はどれだけ拡大しても変わらない。
上から１倍、１０倍、１００倍、１０００倍、１００００倍と拡大した。
二つ目、三つ目の図の目玉がそれぞれの解になっている。
←この図からは、どれだけ拡大しても同じ景色が続く。
（これらの図は【十進BASIC】で作成）
３、見事なフラクタル図形を描く
これを見ると、10000倍以上は同じ景色で、拡大をしていくと1000倍の所で大きく変化する。そしてこれ以上どれだけ拡大しても同じ景色が広がるばかりである。
ただ、複素平面に拡張した時の図形的意味は気になる。
そこでｙ＝ｘ3−１を複素数関数にすると、
f(a＋bi)＝(a＋bi)3−1＝(a3−3ab2−1)＋(3a2b−b3)i
解は、f(a＋bi)が実数になる場合だから、
虚部は、(3a2b−b3)＝b(3a2−b2)＝b(√3a±b)＝0
よって、
b＝0 または b＝±√3a の場合に分けた時の、実部の変化を調べる。
実部を、
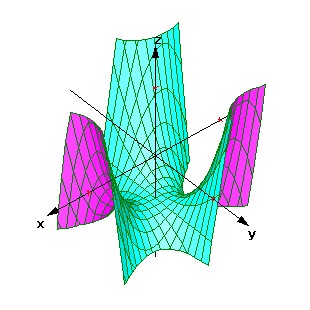
f(ｘ,ｙ)＝ｘ3−3ｘｙ2−1
とおいて、三次元のグラフにすると右図のようになる。
ここで、
b＝0の時は、平面ｘ＝0と平面ｙ＝0との交点(1，0，0)
b＝±√3aの時は、平面ｙ＝±√3ｘとｙ＝0との交点(−0.5,±√3／2，0)が解である。
したがって、解は(ｘ，ｙ)＝(1，0),(−0.5，√3／2),(−0.5，−√3／2)
それぞれの解に対して、ニュートン法を適用していることがわかる。
微分係数は曲面のそれぞれの点における接面になっているのだろう。
次に、
−１〜１までの数値がどのように収束していくのかを調べてみた。
エクセルで収束の数値を計算させ、それを散布図を使ってプロットしてグラフを描き、背景に図を埋め込んでみた。
【エクセルのデータ（１倍）】
【エクセルのデータ（１／５倍）】
（左のグラフに直接数値を入れて、変化を確かめることができます。）
三ヶ所の解に向かって収束する様子を折れ線で表してある。
中には、この範囲から飛び出して、また戻ってきているものもある。
これを見ると、かなり複雑であることがわかる。
あちらこちらの島を飛んでいる数値もある。
複素平面から複素平面への写像を何とか見えるような形で表したいと思ったが、意外と難しいようだ。
ま、その様子をイメージ化したものがこのフラクタルの図なのかもしれない。
しかし、なぜこのような図になるのかはやっぱり不思議である。
ｆ(ｘ)＝ｘ4−1 の図
４、パソコンの進歩
２８年前の１６ビットのパソコンでは１５時間以上かかって描いていた。次の日でないと結果がわからないのである。このパソコンでは数分で描ききる。速度はかなり速くなっている。しかし、考え方やそれをプログラムする方法はそんなに変っていない。進化したのは早さだけ。
でも、この素材は複素平面の性質を探るのにとてもいい教材ではないかと思っている。実数の法則を複素数に拡張する場合の面白い例になるのではないだろうか。
少し根を詰めたら心拍数が上がりめまいがした。先生から、「難しいことをやりすぎだから、もっとぼんやりと過ごさないと良くならないよ。」と言われてしまった。
目次へもどる