オイラーの多面体定理の使い方
― 七角形の不思議 ―
1.オイラーの多面体定理の読み方
S:ところで、疑問が一つあるんですが。
T:何ですか?
S:この前のページで、五角形と六角形と七角形でトーラス(ドーナッツ)を作ったときの式で、
(5χ+6y+7z)/3+(χ+y+z)−(5χ+6y+7z)/2=0
χ−z=0
χ=z
となったけど、この式では七角形はいくつでもいいことになりませんか?
S:そうですよ。七角形が1コでもトーラスができるんでしょうか?
T:前のページで作ったドーナッツは、七角形を10コ使ったけど、これをどれだけ減らせるのかやってみよう。
S:穴をできるだけ小さくしたらどうだろう?
S:七角形を6コ使うと、小さな穴ができるよ。
S:でも、それを広がらせて折り返そうとすると、さらに七角形が必要だよ。


S:なんだかリンゴみたいになったね。
S:最初は七角形を18コ使っていたけど、減らして16コ、さらに10コ。
七角形:18→16→10→
五角形:18→16→10→
S:つまり、まだまだ少なくできる。
S:もしかしたら、六角形だけでトーラスができるんじゃないの?
T:六角形だけで円柱の筒ができるね。それを折り返して上と下をつないだらどうなるのだろう。
S:そうか。ぺしゃんこだけど確かに六角形だけでトーラスはできるね。(なんと、六角形だけで閉曲面ができるのです。)でも、これを膨らませるにはヒモがもっと必要になる。七角形を作ればヒモが増える。まず、七角形を4コにして作ってみよう。


T:上の黄色のリンゴは穴の中に七角形をつくったけど、今度は穴は六角形で作って、折り返すところに2コずつ七角形を作った。
・・・
S:できた!
S:ということは、七角形が1コ(五角形も1コ)でも(膨らんだ)トーラスはできるということですね。
T:つまり、このオイラーの公式は極めて正確にトーラスの状態を表わしているわけだ。このように多角形を折り返したり曲げたりしても変わらない図形の性質を調べることを「トポロジー」というんだ。
S:ヒモを線にしてトーラスの上に図形を描いていくと、六角形だけや七角形と五角形が描けるということですね。
S:ところで、七角形だけで編んでいくと、どんな形になるんだろう?
S:想像もできないよ。決まった形になるのかなぁ?
S:調べてみよう!
2.七角形のみでカゴメ折り
S:何だろう? この形は?


⇒【動画】 回転させます。
S:トーラスとも違うね。いくつも穴があるし、大きさも位置も異なっている。
S:不規則な形だね。
S:まるで、ガウディの建築みたい。
S:これって同じ形になるのかなぁ?
S:二つ作ってみたけど、次の七角形を作る方向によって形がちがってくる。
S:七角形の作る位置を同じにすれば同じ形になるけど、少しでも違うと別の形になる。
S:対称にはならないのかな?
S:どこか対称な点はないかと思ったけど、どこにもなかったよ。
S:一体何だろう?
3.オイラーの定理で考える
T:ここで、例によってオイラーの多面体定理に聞いてみよう。
S:困った時は、オイラーの定理!
T:最初に六角形と七角形のみで多面体を作ると考えてみよう。
そうすると、
(6χ+7y)/3+(χ+y)−(6χ+7y)/2=2
12χ+14y+6χ+6y−18χ−21y=12
y=−12
S:七角形がマイナス12個?
これはどういうことですか?
S:七角形=−五角形と考えたら、五角形が12個だからつじつまはあうね。
T:では、七角形のみだと、どんな式になるのだろう?
S:穴がいっぱいあるから、種数を考えないといけないよ。
S:種数を0,1,2,3,・・・とすると、右辺の値Aは、
A=2,0,−2,−4,・・・
7χ/3+χ−7χ/2=A
(14χ+6χ−21χ)/6=A
χ=−6A
つまり、
種数= 0 1 2 3 4 5・・・
A= 2 0 −2 −4 −6 −8・・・
七角形=−12 0 12 24 36 48・・・
S:これはどういうこと?
S:ドーナッツは七角形だけでは作れないとういうことか。
S:七角形12個で種数2のトーラスができるって言うこと?
S:さっき作ったものは七角形も無限、種数も無限ということかな。
4.種数2のトーラス
S:七角形を12コで種数2のトーラスができるのかな。
S:七角形だけだとガウディの建築になってしまう。やっぱり六角形も入れなくては。
・・・
できた。穴を折り返す所にそれぞれ3コずつ、計12コの七角形と六角形で、種数2のトーラスができた。
(5x+6y+7z)/3+(x+y+z)−(5x+6y+7z)/2=−2
x−z=−12
x=z−12
S:七角形が12の時、五角形は0だ。
T:この定理はみごとですね。


5.その他
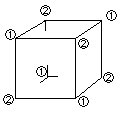
S:正六面体を作ることはできないのですか?
T:六面体の頂点は8なので、12の五角形を等分することはできません。
でも、左図のように五角形を割り振ると、四角柱にはなります。
それから二つの五角形の向きを変えると、やや立方体に近くなります。


S:正八面体も工夫してみました。どうでしょうか。

S:種数2のトーラスをもっときれいにしようと考えて作りました。二つの穴から作り始め、左右対称になるようにしました。七角形は20コ、五角形は8コなので長方形に見えます。


目次へもどる












