弧に対する円周角の代わりに、
弧に対する弧を考えて、
その弧の長さを変えないように動かすと
何が変わらないのだろうか?
円周角の定理の拡張の仕方
― 円周角の定理と中心角の定理の統合 ―
弧に対する円周角の代わりに、 弧に対する弧を考えて、 その弧の長さを変えないように動かすと 何が変わらないのだろうか? |
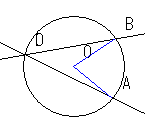
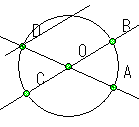 弧に対しての円周角や中心角でなく、弧に対しての対頂角というこのアイディアは、一般化できるのだろうか。
弧に対しての円周角や中心角でなく、弧に対しての対頂角というこのアイディアは、一般化できるのだろうか。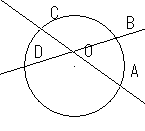 「頂点が円の内部にあるとき、対頂角の大きさが等しければ、切り取られる弧の長さの和は同じである。」
「頂点が円の内部にあるとき、対頂角の大きさが等しければ、切り取られる弧の長さの和は同じである。」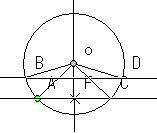
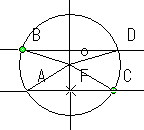 ∠BON=∠AOB+∠AOF=∠DOC+∠COF=∠DONなので、
∠BON=∠AOB+∠AOF=∠DOC+∠COF=∠DONなので、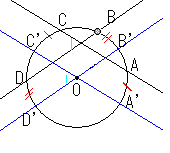 証明
証明| ある弧に対して、円周上に一定の長さの弧を取った時、 二つの弧の両端の点を対角に結んだ時にできる角は一定で、 中心角の合計の半分である。 |