アリが直方体の表面の頂点Pにいます。頂点Aに餌を見つけました。PからAへの最短コースはどれだろう。
S：ピンクが一番短いよ。S：みんな同じだよ。
T：それを確かめるにはどうしたらいいだろうか？
S：長さを測ればいいよ。ピタゴラスの定理を使って。
S：縦・横・高さはわかっている。
S：展開すればいい。
S：どういうこと？
S：こういうように直方体を展開すると、どれが一番短いかすぐわかる。S：直線が最短だから、ピンクだ。
T：これを折り曲げても、長さは変わらないね。
S：折れ曲がっているからわかりにくいので、展開して直線を結べばいいわけか。
T：このアイディアは円錐などの曲面でも使えるね。
S：展開図を描いて直線を結べばいいわけだ。
S：展開の方法は二通りあるよ。どちらも同じになるのかな？
２、ヤギの水飲み
下の図のように、小川が流れています。ヤギが水を飲んで小屋に帰ろうとしています。ヤギは疲れているので早く帰りたい。最短コースはどれでしょう。
S：ヤギのいる所と小屋の真ん中で水を飲めばいいんじゃない。S：ヤギはすぐに水を飲みたいから、垂直に川へ行く。
S：帰りが長くなるよ。
S：どこでもおなじじゃない。
S：さっきは違ったから、今度も最短コースがあるんだよ。
S：展開図は描けないな。
T：展開図は描けないけど、鏡をイメージしてみて。S：光のように反射するということ？
S：わかった。入射角と反射角が同じになるような点だ。
S：そんなのどうやって求めるの。
S：分度器で測ればいい。
T：分度器で測らなくても簡単に作図できるよ。
S：鏡だから、反対側に映るんだ。それを直線で結べばいい。
S：へー。すごい。
S：そうか、この三角形は二等辺三角形だ。
S：これなら、入射角と反射角が等しいこともすぐにわかる。
S：他のコースはこの直線よりも長くなる。
T：光もこうやって反射しているんですよ。
３、アリスの水くみ
アリスは桶に水をくんでから、小屋に行こうとしています。どのコースを選べばいいでしょうか。
S：ヤギの問題と同じではだめなの？T：アリスは桶を持っているんだ。その桶に水を汲んで小屋に行かなくてはならない。水を入れると桶はとても重くなる。
S：水を汲んでから小屋までの道が短いほうがいい。
S：そうだよね。一番短い小屋から垂直の所ではだめなの。
T：アリスは早く帰りたい。そこで、水を汲んだ後のスピードは汲まない前の半分になるとしよう。つまり、時間が2倍になる。
S：同じ速さならヤギの問題と同じだけど、汲んだ後は遅くなるんだから…。
S：小屋に近い所で汲んで、小屋に行った方がいいことは間違いないよ。
S：でもどこかはわからないよ。
T：実は計算できるんだけどね。ちょっと難しいかもしれないけどやってみようか。
まず、アリスが何も持たない時の速さを2ｖとする。桶を持つと速さvになる。
左の図のように長さを決めるよ。この時χを変数と考えて距離を出すと、AM＝√(χ2＋a2) MB＝√((l−χ)2＋ｂ2）
S：ピタゴラスの定理ですね。
T：そうだよ。次はかかった時間を出すよ。
S：時間＝距離÷速さだね。
T：つまり、
√(χ2＋a2) √((l−χ)2＋ｂ2）
T(χ)＝―――――― ＋ ―――――――
2v ｖ
さて、これはどんな関数になるか？
S：ａとｂ、ｌ、ｖは適当な値にしていいんだね。
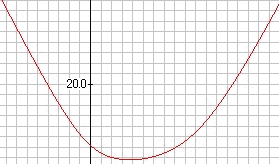
S：上向の二次関数のようになるよ。Uの字型だ。
T：ということは、この関数は最小値を持つということだね。
S：時間が最小になるところを見つければ良いという事ですね。
S：グラフを描けば解りますよ。(グラフが描ける人は飛ばしてもＯＫですよ。)
T：そうなんだが、ここではちょっと面白い方法で考えてみよう。このグラフの最小値では傾きは０になるよね。
S：接線が水平だから傾きが０ですね。
T：ということは、最小値になるχでは、変化の割合が０になりますね。
S：でも、変化の割合は(ｙの増加量)／(χの増加量)でしょ。最小値は点だからχの増加量は０ですよ。
T：そうなんだ。０と考えるとこの割り算はできない。そこで、χの増加量をどんどん小さくしていくとどうなるだろう。
S：０になるよ。
T：では、(ｙの増加量)／(χの増加量)はどうなるだろうか。
S：わからない。
T：それを計算してみるんだ。まずχがΔχ増えると、ｙはT(χ＋Δχ)−T(χ)増えるね。
変化の割合は T(χ＋Δχ)−T(χ) で求まる。このときΔχを限りなく小さくするんだ。
Δχ
S：こんな計算できるの？
T：できるんだ。まずT(χ)を
√((χ＋Δχ)2＋a2)−√(χ2＋a2)
―――――――――――――― と、
2vΔχ
√((l−χ−Δχ)2＋ｂ2）−√((l−χ)2＋ｂ2）
――――――――――――――――――― の二つに分けて考えてみるよ。
ｖΔχ
最初の式の分母分子に√((χ+Δχ)2＋a2)＋√(χ2＋a2)をかけると分子の√が消える。
(χ＋Δχ)2＋a2−(χ2＋a2)
＝――――――――――――――――――
2vΔχ(√((χ＋Δχ)2＋a2)＋√(χ2＋a2))
2χΔχ＋Δχ2
＝―――――――――――――――――― Δχで約分すると、
2vΔχ(√((χ＋Δχ)2＋a2)＋√(χ2＋a2))
2χ＋Δχ
＝―――――――――――――――― ここでΔχを限りなく小さくすると、
2v(√((χ＋Δχ)2＋a2)＋√(χ2＋a2)) 2χΔχ＋Δχ2は０とみなせる。
2χ χ
＝―――――― ＝ ――――――
4v√(χ2＋a2) 2v√(χ2＋a2)
同様にもう一つの方も計算すると、
√((l−χ−Δχ)2＋ｂ2）−√((l−χ)2＋ｂ2）
―――――――――――――――――――― Δχを限りなく小さくすると、
ｖΔχ
−(ｌ−χ)
＝―――――――――
ｖ√((l−χ)2＋ｂ2）
そして、２つの式を合体させ、Δχを限りなく小さくすると、
T(χ＋Δχ)−T(χ) χ ｌ−χ
＝―――――――― ＝ ――――――― − ――――――――― ＝０
Δχ 2ｖ√(χ2＋a2)) ｖ√((l−χ)2＋ｂ2）
つまり、
χ ｌ−χ
―――――― ＝ ――――――――― の時に時間は最小値になる。
2ｖ√(χ2＋a2) ｖ√((l−χ)2＋ｂ2）
さらにこれは、
ｖχ 2ｖ(ｌ−χ)
――――― ＝ ―――――――― と変形できる。
√(χ2＋a2) √((l−χ)2＋ｂ2）
S：これを解くと、χ＝が出るの？
T：ａ、ｂ、ｖの値が決まれば出るよ。さらに、これを三角関数であらわすと、
ｖｓｉｎθ＝2ｖｓｉｎγ これを分数で表すと、
ｓｉｎθ
―――― ＝２ のとき時間は最小になる。
ｓｉｎγ
S：速さがｗとｖだったら、ｓｉｎθ／ｓｉｎγ＝ｗ／ｖ（屈折の法則）ですね。
S：複雑すぎるよ。
T：中学生にもわかる微分だよ。（微分ができる人はもっと簡単な計算で求めることができます。）
S：アリスはそんな計算はできないよ。
S：ところで、この図を見ると光の屈折をイメージするな。
S：さっきは反射、今度は屈折か。
T：実は３５0年前にフェルマーという人が、光の反射の考えを屈折にも当てはめることができるはずだと考えて、同じ計算をしているんだ。
４、フェルマーの最小原理
T：光が水の中に入るとき、屈折するのはなぜだろうか。
S：理科の実験でやったよ。光が違う物質を通ると屈折が起こるんだ。T：それは、まさにアリスと同じことが起きているんだ。光がアリス。
S：空気中よりも水の中の方が光は遅くなるということなの。
T：うん。光は水の中では、速さが約３／４になる。ｓｉｎθ／ｓｉｎγ＝４／３だ。これが屈折率。
S：光は、水の中では桶を担いでいるからできるだけ楽をしようと考えているの？
T：そうなんだ。これを発見したのがフェルマーで、彼は「楽をする」と言う代わりに、「光はある場所からある場所へ行くときに、最小の時間で到達できるコースを進む。」という原理を考えた。この原理を「フェルマーの最小原理」という。
S：屈折した方が時間は短くなるわけか。
S：でも、光はその最短のコースをどうやって選ぶの？
T：それが不思議なんだね。光は、はじめから最短のコースがわかっているとしか言いようがないんだ。
S：アリスだって、どこが最小時間か計算できないよ。
S：光は全てのコースを通っていて、どこが最短かすでに確かめているんじゃないの。
Ｔ：いい考えだね。同じように、ファインマンという人は、光は全ての方向に反射・屈折していて、目的の場所に至るコースは無限にあるのではないかと考えた。
S：それが、どうして最短コースだけになるの？T：最短コース以外の場所では、距離が長くなるので光の波長がずれ、互いに干渉しあい打ち消しあってしまうからだ。
S：それなら、最短コースの付近だって打ち消しあうんではないの？
T：さっき、T(χ)は上向の二次関数のようになったでしょ（左のグラフ。正確にはV字型で、最小値の付近だけゆるやか。なお、このグラフはヤギの水飲みの場合を式にした、ｙ＝√(x2＋ａ2）＋√((ｌ−ｘ)2＋ｂ2）のグラフ）。最小値の近辺では距離の変化が少ない。その他のところでは、χが変わると距離も変化する。そうすると、波長の位相がずれるから、互いに打ち消しあうけど、最小値のところでは変化が少ないから、逆に互いに強め合うということになるのです。
S：そうか。光は波だから波長がずれると、消えるわけか。
S：そういえば、雑音を消すために位相をずらした音を出すことによって打ち消す装置があるよ。
S：ところで入射角は媒質の平面との角度ではなく、垂直線との角度なのはなぜ？
T：入射角０度という時を考えてみて。
S：その時、屈折角も０度だ。
T：その時、真横から当てたほうが自然か、垂直に当てたほうが自然か。
S：垂直の方が自然だな。角度を増やしていくと屈折がおきる。
T：真横からは屈折せずに反射するもんね。そして計算するときも垂直線の方が計算しやすい。
T：このSFをぜひ読んでみて。とても面白い。このフェルマーの最小原理をわかり易く説明しているし、何よりもストーリーが面白い。早川書房「あなたの人生の物語」著者：テッド・チャン。もう一つ「数学が解き明かした物理の法則」べレ出版・大上雅史・和田純夫著。目からうろこが落ちる。数学がどうやって発展してきたのかもわかる。フェルマーの最小原理について詳しく書いているよ。